阅读更多

1 基本概念

基于TensorFlow的神经网络（Neural Network，NN）

用张量表示数据
用计算图搭建神经网络
用会话执行计算图，优化线上的权重(参数)，得到模型

1.1 张量

张量就是多维数组（列表），用“阶”表示张量的维度

0阶张量称作标量，表示一个单独的数
- $S = 123$
1阶张量称作向量，表示一个一维数组
- $V = [1,2,3]$
2阶张量称作矩阵，表示一个二维数组，它可以有i行j列个元素，每个元素可以用行号和列号共同索引到
- $m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]$
判断张量是几阶的，就通过张量右边的方括号数

1.2 数据类型

TensorFlow的数据类型有

tf.int8
tf.int16
tf.int32
tf.int64
tf.float32
tf.double
…

1.3 计算图

计算图(Graph)是搭建神经网络的计算过程，是承载一个或多个计算节点的一张图，只搭建网络，不运算

神经网络的基本模型是神经元，神经元的基本模型其实就是数学中的乘、加运算。神经元的形式化定义如下$$f(\sum_{i}{x_{i}w_{i}}+b)$$

$f$为激活函数，引入非线性激活因素，提高模型的表达能力

举个简单的例子，给定如下计算图

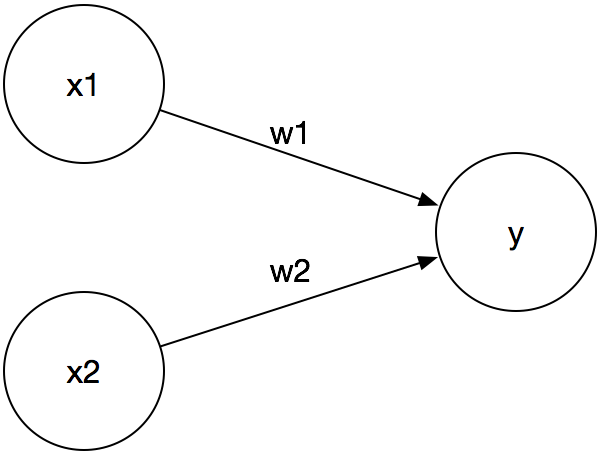
我们用TensorFlow实现上述计算图

import TensorFlow as tf

# 定义张量
x = tf.constant([[1.0, 2.0]])
w = tf.constant([[3.0], [4.0]])

# 计算图
y = tf.matmul(x, w)
print(y)

1.4 会话

会话(Session)用于执行计算图中的节点运算

继续上一小节的例子，我们用会话执行计算图中的节点运算

1
2
3

# 执行计算图中的节点运算
with tf.Session() as sess:
    print(sess.run(y))

2 神经网络的参数

神经网络的参数是指神经元线上的权重w，用变量表示，一般会先随机生成这些参数。生成参数的方法是让w等于tf.Variable，把生成的方式写在括号里

神经网络中常用的生成随机数/数组的函数有：

tf.random_normal()：生成正态分布随机数
- w = tf.Variable(tf.random_normal([2,3], stddev=2, mean=0, seed=1))
- stddev表示标准差
- mean表示均值
- seed表示随机数种子
tf.truncated_normal()：生成去掉过大偏离点的正态分布随机数
- w = tf.Variable(tf.Truncated_normal([2,3], stddev=2, mean=0, seed=1))
- 如果随机出来的数据偏离平均值超过两个标准差，这个数据将重新生成
tf.random_uniform()：生成均匀分布随机数
- w = random_uniform(shape=7, minval=0, maxval=1, dtype=tf.int32，seed=1
- 表示从一个均匀分布[minval maxval)中随机采样
tf.zeros：表示生成全0数组
tf.ones：表示生成全1数组
tf.fill：表示生成全定值数组
tf.constant：表示生成直接给定值的数组

3 神经网络的实现过程综述

神经网络的搭建一般按照如下过程进行

准备数据集，提取特征，作为输入喂给神经网络（Neural Network，NN）
搭建NN结构，从输入到输出（先搭建计算图，再用会话执行）
- NN前向传播算法–>计算输出
大量特征数据喂给NN，迭代优化NN参数
- NN反向传播算法优化参数训练模型
使用训练好的模型预测和分类

4 前向传播

前向传播是指搭建模型的计算过程，让模型具有推理能力，可以针对一组输入给出相应的输出

举个简单的例子，给出如下神经网络。由输入$\vec{X}$经过神经网络计算得到$\vec{Y}$的过程就称为前向传播过程

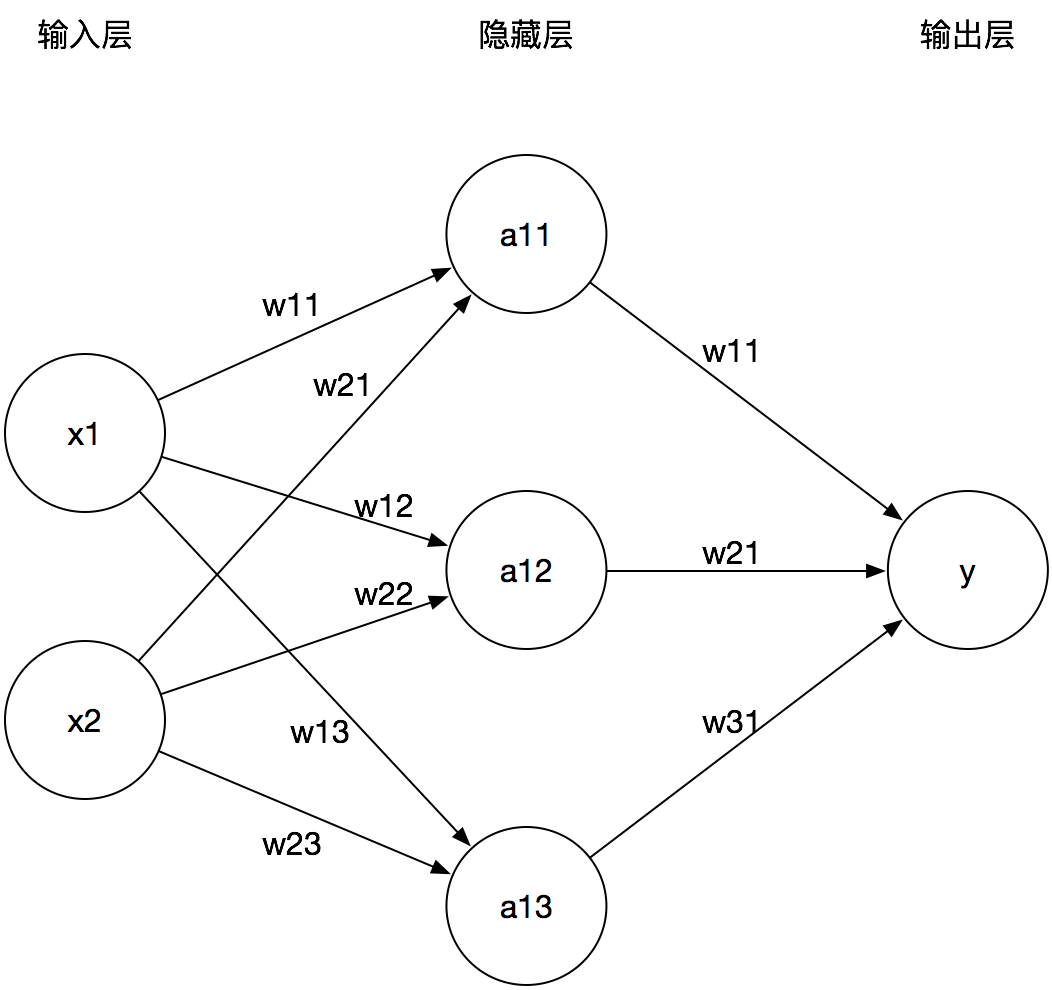
该神经网络可表示成如下形式

$$\vec{Y} = \vec{X} \cdot \vec{W^{1}} \cdot \vec{W^{2}}$$

$\vec{X}$是输入向量
$\vec{W^{1}}$是2行3列的参数矩阵
$\vec{W^{2}}$是3行1列的参数矩阵
$\vec{Y}$是输出向量

上述例子的前向传播过程的TensorFlow描述（变量初始化、计算图节点运算都要用会话实现）

变量初始化：在sess.run函数中用tf.global_variables_initializer()汇总所有待优化变量

1 2	init_op = tf.global_variables_initializer() sess.run(init_op)

计算图节点运算：在sess.run函数中写入待运算的节点

1	sess.run(y)

喂数据：用tf.placeholder占位，在sess.run函数中用feed_dict喂数据（以这种方式实现计算图与运算的分离）

1
2
3

# 一组数据
x = tf.placeholder(tf.float32, shape=(1, 2))
sess.run(y, feed_dict={x: [[0.5,0.6]]})

1
2
3

# 多组数据
x = tf.placeholder(tf.float32, shape=(None, 2))
sess.run(y, feed_dict={x: [[0.1,0.2],[0.2,0.3],[0.3,0.4],[0.4,0.5]]})

4.1 完整程序

喂一组数据

# coding:utf-8
import TensorFlow as tf

# 定义输入和参数
x = tf.placeholder(tf.float32, shape=(1, 2))
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 用会话计算结果
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print("y in tf3_3.py is:\n", sess.run(y, feed_dict={x: [[0.7, 0.5]]}))

喂多组数据

# coding:utf-8
import TensorFlow as tf

# 定义输入和参数
x = tf.placeholder(tf.float32, shape=(None, 2))
w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

# 定义前向传播过程
a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 用会话计算结果
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)
    print("y in tf3_3.py is:\n", sess.run(y, feed_dict={x: [[0.1,0.2],[0.2,0.3],[0.3,0.4],[0.4,0.5]]}))

5 反向传播

反向传播是指训练模型参数，在所有参数上用梯度下降，使NN模型在训练数据上的损失函数最小

5.1 损失函数

损失函数(loss)：计算得到的预测值y与已知答案y_的差距

损失函数的计算有很多方法，均方误差MSE是比较常用的方法之一

$$MSE(y\_, y)=\frac{\sum_{i=1}^{n}{(y-y\_)^2}}{n}$$

在TensorFlow中可以表示为loss_mse = tf.reduce_mean(tf.square(y_ - y))

5.2 反向传播训练方法

反向传播训练方法是指，以减小loss值为优化目标。有梯度下降、momentum优化器、adam优化器等优化方法。这三种优化方法用TensorFlow的函数可以表示为

train_step=tf.train.GradientDescentOptimizer(learning_rate).minimize(loss)
train_step=tf.train.MomentumOptimizer(learning_rate, momentum).minimize(loss)
train_step=tf.train.AdamOptimizer(learning_rate).minimize(loss)

5.2.1 学习率

优化器中都需要一个叫做学习率的参数，使用时，如果学习率选择过大会出现震荡不收敛的情况，如果学习率选择过小，会出现收敛速度慢的情况

5.2.2 随机梯度下降算法

随机梯度下降算法，使参数沿着梯度的反方向，即总损失减小的方向移动，实现更新参数

$$\theta_{n+1} = \theta_{n} - \alpha \frac{\partial{J(\theta_{n})}}{\theta_{n}}$$

$J(\theta_{n})$表示损失函数
$\theta$表示参数，其下标表示迭代次数
$\alpha$表示学习率

5.2.3 Momentum算法

该算法在更新参数时，利用了超参数，参数更新公式如下

$$\begin{split} d_{i} &= \beta d_{i-1} + g(\theta_{i-1}) \\ \theta_{i} &= \theta_{i-1} - \alpha d_{i} \end{split}$$

$\alpha$表示学习率
$\beta$表示超参数
$g(\theta_{i-1}) $表示损失函数的梯度

5.2.4 自适应学习率的优化算法

Adam算法和随机梯度下降算法不同。随机梯度下降算法保持单一的学习率更新所有的参数，学习率在训练过程中并不会改变。而Adam算法通过计算梯度的一阶矩估计和二阶矩估计而为不同的参数设计独立的自适应性学习率

5.3 完整程序

# coding:utf-8

import TensorFlow as tf
import numpy as np

BATCH_SIZE = 8
seed = 23455

# 基于seed产生随机数
rng = np.random.RandomState(seed)

# 随机数返回32行2列的矩阵，表示32组体积和重量作为输入数据集
X = rng.rand(32, 2)

# 产生数据标签
Y = [[int(x0 + x1 < 1)] for (x0, x1) in X]

print("X:\n", X)
print("Y:\n", Y)

# 1 定义神经网络的输入、参数和输出，定义前向传播过程
x = tf.placeholder(tf.float32, shape=(None, 2))
y_ = tf.placeholder(tf.float32, shape=(None, 1))

w1 = tf.Variable(tf.random_normal([2, 3], stddev=1, seed=1))
w2 = tf.Variable(tf.random_normal([3, 1], stddev=1, seed=1))

a = tf.matmul(x, w1)
y = tf.matmul(a, w2)

# 2 定义损失函数及反向传播方法
loss = tf.reduce_mean(tf.square(y - y_))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)
# train_step = tf.train.MomentumOptimizer(0.001).minimize(loss)
# train_step = tf.train.AdamOptimizer(0.001).minimize(loss)

# 3 生成会话，训练STEPS轮

with tf.Session() as sess:
    init_op = tf.global_variables_initializer()
    sess.run(init_op)

    # 输出目前（未经训练）的参数取值
    print("w1:\n", sess.run(w1))
    print("w1:\n", sess.run(w2))
    print("\n")

    # 训练模型
    STEPS = 3000
    for i in range(STEPS):
        start = (i * BATCH_SIZE) % 32
        end = start + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})
        if i % 500 == 0:
            total_loss = sess.run(loss, feed_dict={x: X, y_: Y})
            print("After %d training step(s), loss on all data is %g" % (i, total_loss))

    # 输出训练后的参数取值
    print("\n")
    print("w1:\n", sess.run(w1))
    print("w1:\n", sess.run(w2))

6 参考

人工智能实践：TensorFlow笔记-曹健

Liuye Notebook

TensorFlow-搭建神经网络