阅读更多

1 自顶向下分析概述

自定向下分析的定义如下

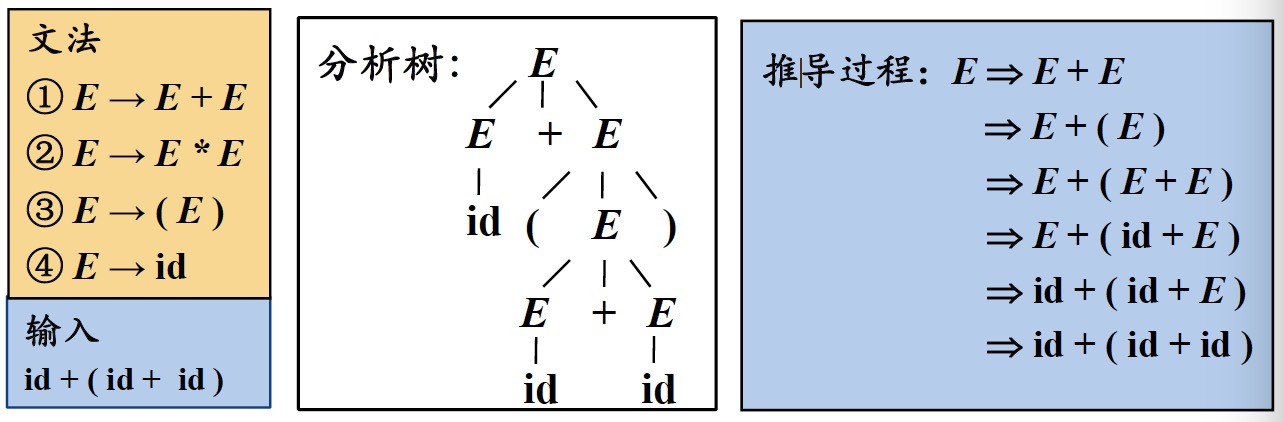
从分析树的顶部（根节点）向底部（叶节点）方向构造分析树
可以看成是从文法开始符号S推导出词串$w$的过程
每一步推导中，都需要做两个选择
- 替换当前句型中的哪个非终结符
- 用该非终结符的哪个候选式进行替换

1.1 最左推导(Left-most Derivation)

最左推导定义：总是选择每个句型的最左非终结符进行替换

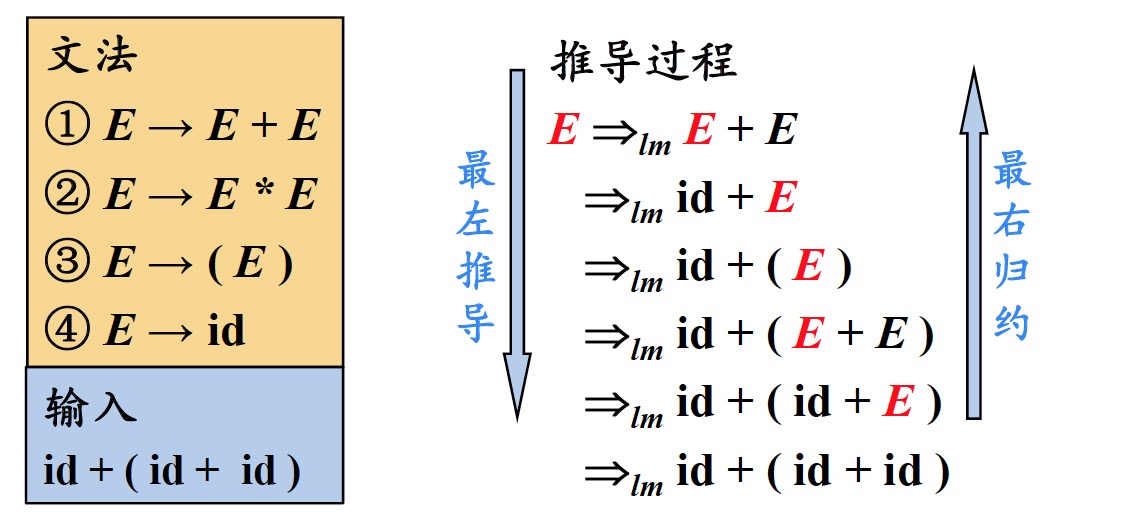
如果$S \Rightarrow ^*_{lm} \alpha$，则称$\alpha$是当前文法的最左句型(left-sentential form)

1.2 最右推导(Right-most Derivation)

最右推导定义：总是选择每个句型的最右非终结符进行替换

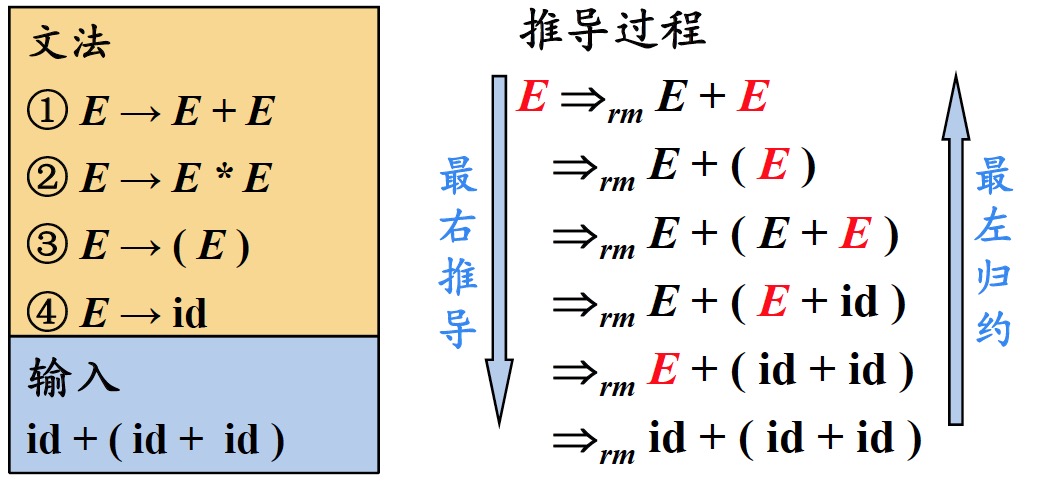
在自底向上的分析中，总是采用最左归约的方式，因此把最左归约称为规范归约，而最右推导相应地称为规范推导

1.3 最左推导和最右推导的唯一性

最左推导和最右推导都是唯一的

1.4 自顶向下的语法分析采用最左推导方式

即

总是选择每个句型的最左非终结符进行替换
根据输入流中的下一个终结符，选择最左非终结符的一个候选式

1.5 自顶向下语法分析的通用形式

递归下降分析(Recursive-Descent Parsing)

由一组过程组成，每个过程对应一个非终结符
从文法开始符号$S$对应的过程开始，其中递归调用文法中其它非终结符对应的过程。如果$S$对应的过程体恰好扫描了整个输入串，则成功完成语法分析
缺点：可能需要回溯(backtracking)，导致效率较低

void A() {
    选择一个A产生式，A → X1X2...Xk
    for( i = 1 to k ) {
        if ( Xi是一个非终结符号)
            调用过程Xi();
        else if(Xi等于当前的输入符号a)
            读入下一个输入符号;
        else /*发生了一个错误*/;
    }
}

预测分析(Predictive Parsing)

预测分析是递归下降分析技术的一个特例，通过在输入中向前看固定个数（通常是一个）符号来选择正确的$A-$产生式
- 可以对某些文法构造出向前看$k$个输入符号的预测分析器，该类文法有时也称为$LL(k)$文法类
预测分析不需要回溯，是一种确定的自顶向下分析方法

2 文法转换

2.1 问题1

同一非终结符的多个候选式存在共同前缀，将导致回溯现象

例如，给定文法$G$

$$\begin{split} S &\to aAd | aBe \\ A &\to c \\ B &\to b \end{split}$$

输入$abc$

2.2 问题2

左递归文法会使递归下降分析器陷入无限循环

如果一个文法中有一个非终结符$A$使得对某个串$\alpha$存在一个推导$A \Rightarrow ^+ A \alpha$ ，那么这个文法就是左递归（一步或多步）
含有$A \to A \alpha$形式产生式的文法称为是直接左递归(immediate left recursive)
经过两步或两步以上推导产生的左递归称为是间接左递归

例如，给定文法$G$

$$\begin{split} E &\to E+T | E-T | T \\ T &\to T*F | T/F | F \\ F &\to (E) | id \end{split}$$

$id+id*id$

2.3 消除直接左递归

首先，以一个例子来进行说明，有如下产生式

$$A \to A \alpha | \beta (\alpha \ne \varepsilon, \beta 不以A开头)$$

在进行递归下降分析时，会产生如下循环

$$\begin{split} A &\Rightarrow A \alpha \\ &\Rightarrow A \alpha \alpha \\ &\Rightarrow A \alpha \alpha \alpha \\ &... \\ &\Rightarrow A \alpha ... \alpha \\ &\Rightarrow \beta \alpha ... \alpha \end{split}$$

因此，与该产生式等价的正则表达式为：$r = \beta \alpha ^*$，从而可以将该产生式进行改写

$$\begin{split} A &\to \beta A^{\prime} \\ A^{\prime} &\to \alpha A^{\prime} | \varepsilon \end{split}$$

事实上，这种消除过程就是把左递归转换成了右递归

2.3.1 消除直接左递归的一般形式

一般形式如下：

$$\begin{split} A &\to A \alpha_1 | A \alpha_2 | ... | A \alpha_n | \beta_1 | \beta_2 | ... | \beta_m (\alpha_i \ne \varepsilon, \beta_j 不以A开头) \\ &\Downarrow \\ A &\to \beta_1 A^{\prime} | \beta_2 A^{\prime} | ... | \beta_m A^{\prime} \\ A^{\prime} &\to \alpha_1 A^{\prime} | \alpha_2 A^{\prime} | ... | \alpha_n A^{\prime} | \varepsilon \end{split}$$

消除左递归是要付出代价的——引进了一些非终结符和$\varepsilon -$产生式

2.4 消除间接左递归

首先，以一个例子来进行说明，有如下产生式

$$\begin{split} S &\to Aa | b \\ A &\to Ac | Sd | \varepsilon \end{split}$$

在进行递归下降分析时，会产生如下循环

$$\begin{split} S &\Rightarrow Aa \\ &\Rightarrow Sda \\ &\Rightarrow Aada \\ &\Rightarrow Sdada \\ &... \end{split}$$

为了消除这种间接左递归，我们将$S$的定义代入$A-$产生式，得到

$$A \to Ac | Aad | bd | \varepsilon$$

这便是$A-$的直接左递归，因此根据上一小节的方法进行消除，得到

$$\begin{split} A &\to bdA^{\prime} | A^{\prime} \\ A^{\prime} &\to c A^{\prime} | ad A^{\prime} | \varepsilon \end{split}$$

2.5 消除左递归算法

输入：不含循环推导（即形如$A \Rightarrow ^+ A$的推导）和$\varepsilon -$产生式的文法$G$
输出：等价的无左递归文法
方法：

2.6 提取左公因子(Left Factoring)

通过改写产生式来推迟决定，等读入了足够多的输入，获得足够信息后再做出正确的选择

$$\begin{split} S &\to aAd | aBe \\ A &\to c \\ B &\to b \\ &\Downarrow \\ S &\to aS^{\prime} \\ S^{\prime} &\to Ad | Be \\ A &\to c \\ B &\to b \\ \end{split}$$

2.6.1 提取左公因子算法

输入：文法$G$
输出：等价的提取了左公因子的文法
方法：

3 $LL(1)$文法

3.1 $S\_$文法

预测分析法的工作过程

从文法开始符号出发，在每一步推导过程中根据当前句型的最左非终结符$A$和当前输入符号$a$，选择正确的$A-$产生式。为保证分析的确定性，选出的候选式必须是唯一的

$S\_$文法（简单的确定性文法，Korenjak & Hopcroft，1966）

每个产生式的右部都以终结符开始
同一非终结符的各个候选式的首终结符都不同
$S\_$文法不含$\varepsilon$产生式

什么时候可以使用$\varepsilon$产生式呢？

如果当前某非终结符$A$与当前输入符$a$不匹配时，若存在$A \to \varepsilon$，可以通过检查$a$是否可以出现在$A$的后面，来决定是否使用产生式$A \to \varepsilon$（若文法中无$A \to \varepsilon$ ，则应报错）

3.2 非终结符的后继符号集

非终结符$A$的后继符号集定义：可能在某个句型中紧跟在$A$后边的终结符$a$的集合，记为$FOLLOW(A)$

$$FOLLOW(A) = \{ a | S \Rightarrow^* \alpha A a \beta, a \in V_T,\; \alpha, \beta \in (V_T \cup V_N)^* \}$$

如果A是某个句型的的最右符号，则将结束符$\$$添加到$FOLLOW(A)$中

例如，给定以下产生式

$$\begin{split} S &\to aBC \\ B &\to bC \\ B &\to dB \\ B &\to \varepsilon \\ C &\to c \\ C &\to a \end{split}$$

可以推导出$FOLLOW(B)=\{ a,c \}$

因此，假设当前匹配到$B$

输入符号为$b$：选择$B \to bC$产生式
输入符号为$d$：选择$B \to dB$产生式
输入符号为$a$或$c$：选择$B \to \varepsilon$产生式

3.3 生产式的可选集

产生式$A \to \beta$的可选集是指可以选用该产生式进行推导时对应的输入符号的集合，记为：$$SELECT(A \to \beta)$$

$SELECT(A \to a \beta) = \{ a \}$
$SELECT(A \to \varepsilon) = FOLLOW(A)$

$q\_$文法

每个产生式的右部或为$\varepsilon$，或以终结符开始
具有相同左部的产生式有不相交的可选集
$q\_$文法不含右部以非终结符打头的产生式

3.4 串首终结符集

串首终结符：串首第一个符号，并且是终结符。简称首终结符

给定一个文法符号串$\alpha$，$\alpha$的串首终结符集$FIRST(\alpha)$被定义为：可以从$\alpha$推导出的所有串首终结符构成的集合。如果$\alpha \Rightarrow^* \varepsilon$，那么$\varepsilon$也在$FIRST(\alpha)$中

对于$\forall \alpha \in (V_T \cup V_N)^+, FIRST(\alpha) = \{ a | \alpha \Rightarrow^* a \beta, a \in V_T, \beta \in (V_T \cup V_N)^* \}$
如果$\alpha \Rightarrow^* \varepsilon$，那么$\varepsilon \in FIRST(\alpha)$

产生式$A \to \alpha$的可选集$SELECT$

如果$\varepsilon \notin FIRST(\alpha)$，那么$SELECT(A \to \alpha) = FIRST(\alpha)$
如果$\varepsilon \in FIRST(\alpha)$，那么$SELECT(A \to \alpha) = ( FIRST(\alpha) - \{ \varepsilon \} ) \cup FOLLOW(A)$

3.5 $LL(1)$文法

文法$G$是$LL(1)$的，当且仅当$G$的任意两个具有相同左部的产生式$A \to \alpha | \beta$满足下面的条件

如果$\alpha$和$\beta$均不能推导出$\varepsilon$，则$FIRST(\alpha) \cap FIRST(\beta) = \Phi$
$\alpha$和$\beta$至多有一个能推导出$\varepsilon$
- 如果$\beta \Rightarrow^* \varepsilon$，则$FIRST(\alpha) \cap FIRST(A) = \Phi$
- 如果$\alpha \Rightarrow^* \varepsilon$，则$FIRST(\beta) \cap FIRST(A) = \Phi$

上述规则简言之：同一非终结符的各个产生式的可选集互不相交

其中，$LL(1)$含义解释如下

第一个$L$表示从左向右扫描输入
第二个$L$表示产生最左推导
1表示在每一步中只需要向前看一个输入符号来决定语法分析动作

4 参考

《MOOC-编译原理-陈鄞》

Liuye Notebook

编译原理-语法分析1