阅读更多

1 活跃变量分析

活跃变量

对于变量$x$和程序点$p$，如果在流图中沿着从$p$开始的某条路径会引用变量$x$在$p$点的值，则称变量$x$在点$p$是活跃（live）的，否则称变量$x$在点$p$是不活跃（dead）的

1.1 活跃变量信息的主要用途

删除无用赋值

无用赋值：如果$x$在点$p$的定值在基本块内所有后继点都不被引用，且$x$在基本块出口之后又是不活跃的，那么$x$在点$p$的定值就是无用的

为基本块分配寄存器

如果所有寄存器都被占用，并且还需要申请一个寄存器，则应该考虑使用已经存放了死亡值的寄存器，因为这个值不需要保存到内存
如果一个值在基本块结尾处是死的就不必在结尾处保存这个值

1.2 活跃变量的传递函数

活跃变量是一个典型的逆向数据流问题

$$IN[B] = f_B(OUT[B]$$

其中，$f_B(x) = use_B \cup (x-def_B)$

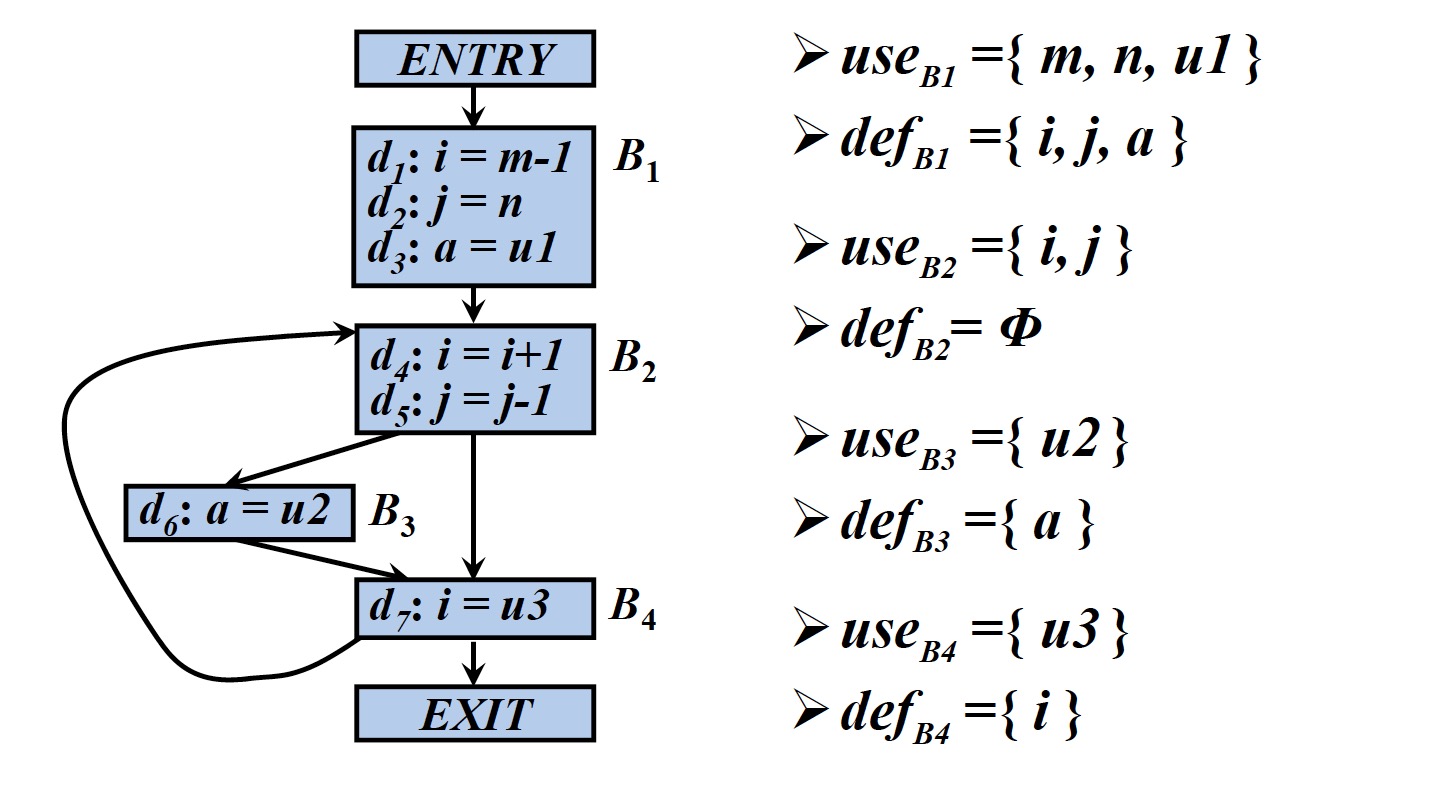
$def_B$：在基本块B中定值，但是定值前在B中没有被引用的变量的集合
$use_B$：在基本块B中引用，但是引用前在B中没有被定值的变量集合

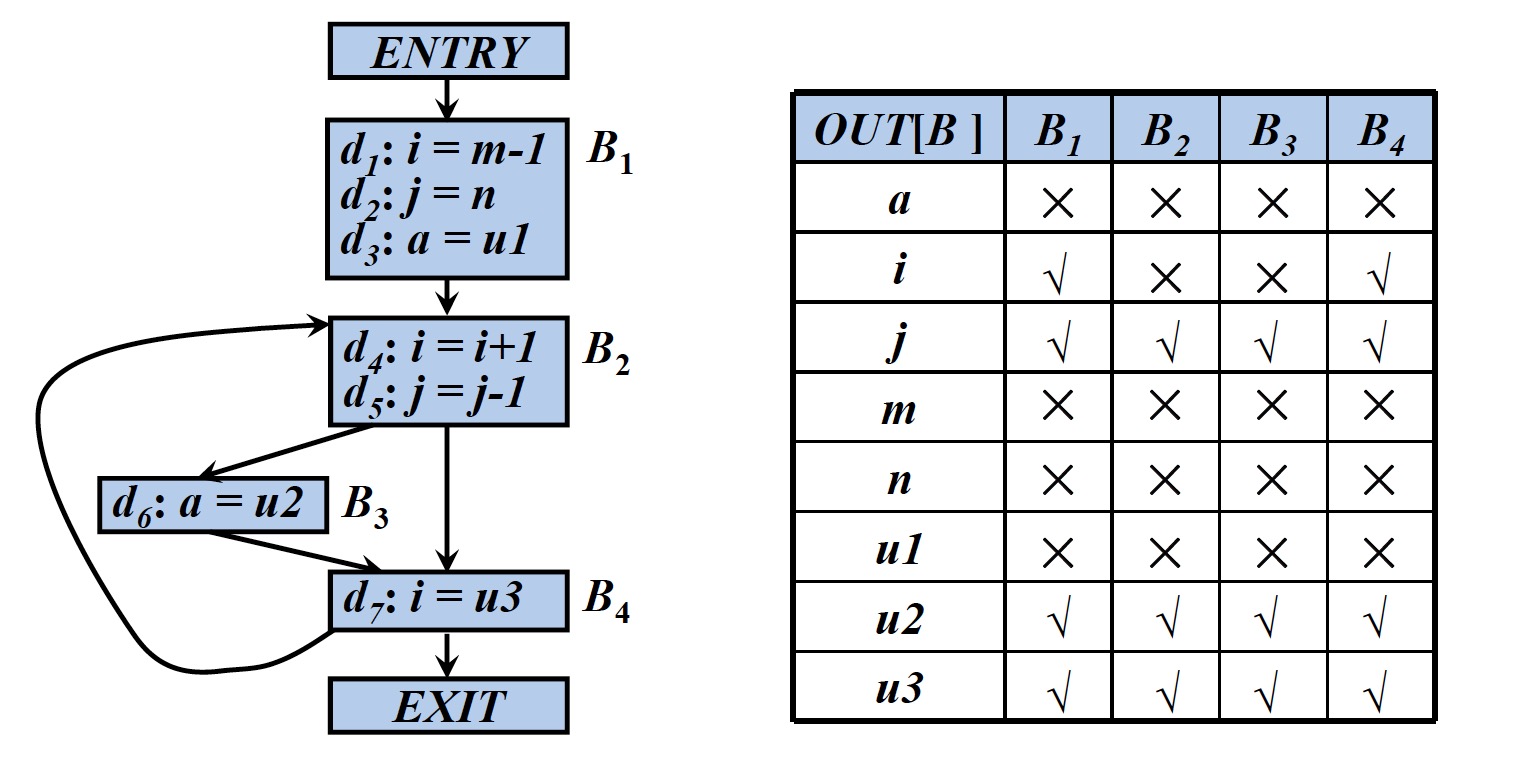
1.3 活跃变量数据流方程

符号及其说明

$IN[B]$：在基本块B的入口处的活跃变量集合
$OUT[B]$：在基本块B的出口处的活跃变量集合

方程

$IN[EXIT] = \Phi$
$IN[B] = f_B(OUT[B]） ( B \ne EXIT )$
$f_B(x) = use_B \cup (x-def_B)$
$OUT[B]= \cup_{S是B的一个后继}\;\;\;\;\;\;\;\;IN[S], ( B \ne EXIT )$

1.4 计算活跃变量的迭代算法

输入：流图G，其中每个基本块B的$use_B$和$def_B$都已计算出来

输出：$IN[B]$和$OUT[B]$

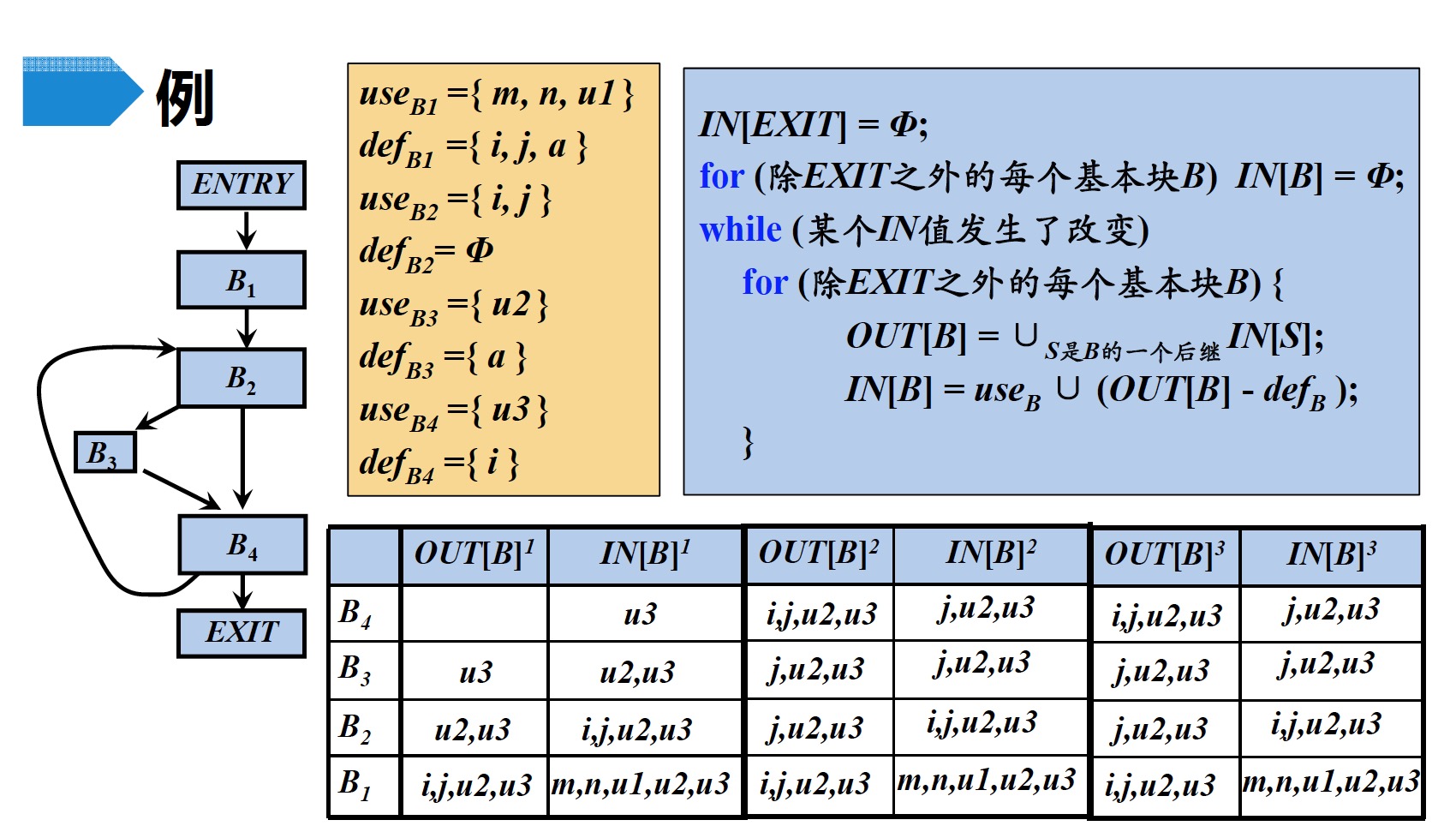
方法：

例子

1.5 定值-引用链(Definition-Use Chains)

定值-引用链：设变量$x$有一个定值$d$，该定值所有能够到达的引用$u$的集合称为$x$在$d$处的定值-引用链，简称$du$链

如果在求解活跃变量数据流方程中的$OUT[B]$时，将$OUT[B]$表示成从B的末尾处能够到达的引用的集合，那么，可以直接利用这些信息计算基本块B中每个变量$x$在其定值处的$du$链

如果B中$x$的定值$d$之后有$x$的第一个定值$d^{\prime}$，则$d$和$d^{\prime}$之间$x$的所有引用构成$d$的$du$链
如果B中$x$的定值$d$之后没有$x$的新的定值，则B中$d$之后$x$的所有引用以及$OUT[B]$中$x$的所有引用构成$d$的$du$链

2 可用表达式分析

可用表达式

如果从流图的首节点到达程序点$p$的每条路径都对表达式$x\;op\;y$进行计算，并且从最后一个这样的计算到点$p$之间没有再次对$x$或$y$定值，那么表达式$x\;op\;y$在点$p$是可用的(available)

表达式可用的直观意义

在点p上，x op y已经在之前被计算过，不需要重新计算

2.1 可用表达式信息的主要用途

消除全局公共子表达式
进行复制传播
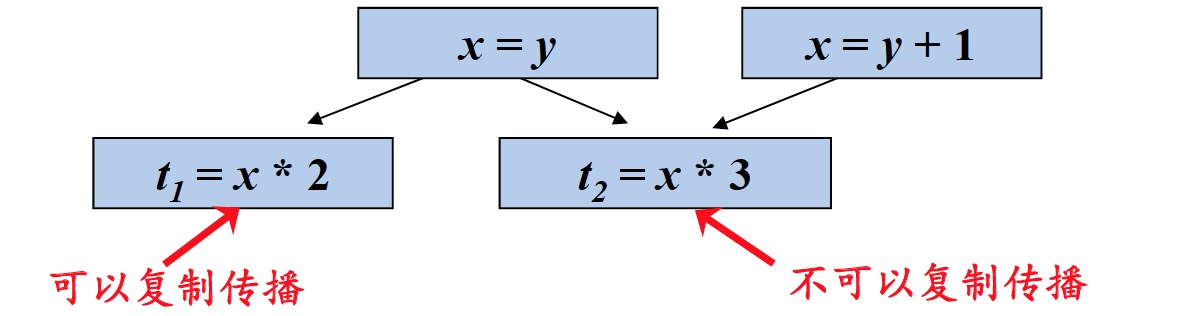
- 在$x$的引用点$u$可以用$y$代替$x$的条件：从流图的首节点到达u的每条路径都存在复制语句$x = y$，并且从最后一条复制语句$x = y$到点$u$之间没有再次对$x$或$y$定值（就是可用表达式的定义）

2.2 可用表达式的传递函数

对于可用表达式数据流模式而言，如果基本块B对$x$或者$y$进行了(或可能进行)定值，且以后没有重新计算$x\;op\;y$，则称B杀死表达式$x\;op\;y$。如果基本块B对$x\;op\;y$进行计算，并且之后没有重新定值$x$或$y$，则称B生成表达式$x\;op\;y$

传递函数定义如下：

$f_B(x)= e\_gen_B ∪(x- e\_kill_B)$
$e\_gen_B$ ：基本块B所生成的可用表达式的集合
$e\_kill_B$ ：基本块B所杀死的U中的可用表达式的集合
$U$：所有出现在程序中一个或多个语句的右部的表达式的全集

2.3 $e\_gen_B$的计算

初始化：$e\_gen_B = \Phi$

顺序扫描基本块的每个语句：$z = x\;op\;y$

把$x\;op\;y$加入$e\_gen_B$
从$e\_gen_B$中删除和$z$相关的表达式

上述两个操作顺序不能颠倒

2.4 $e\_kill_B$的计算

初始化：$e\_kill_B = \Phi$

顺序扫描基本块的每个语句：$z = x\;op\;y$

从$e\_kill_B$中删除表达式$x\;op\;y$
把所有和$z$相关的表达式加入到$e\_kill_B$中

2.5 可用表达式的数据流方程

符号及其说明

$IN[B]$：在B的入口处可用的$U$中的表达式集合
$OUT[B]$：在B的出口处可用的$U$中的表达式集合

方程

$OUT[ENTRY]= \Phi$
$OUT[B]=f_B(IN[B]), ( B \ne ENTRY )$
- $f_B(x)= e\_gen_B \cup (x- e\_kill_B)$
$IN[B]= \cap_{P是B的一个前驱}\;\;\;\;\;\;\;OUT[P], ( B \ne ENTRY )$

2.6 计算可用表达式的迭代算法

输入：流图G，其中每个基本块B的$e\_gen_B$和$e\_kill_B$都已计算出来

输出：$IN[B]$和$OUT[B]$

方法:

2.6.1 为什么将$OUT[B]$集合初始化为$U$

将OUT集合初始化为$\Phi$局限性太大

如果$OUT[B_2]^0 = \Phi$

那么$IN[B_2]^1= OUT[B_1]^1 \cap OUT[B_2]^0 = \Phi$

如果$OUT[B_2]^0 = U$

那么$IN[B_2]^1= OUT[B_1]^1 \cap OUT[B_2]^0 = OUT[B_1]$

3 参考

《MOOC-编译原理-陈鄞》

Liuye Notebook

编译原理-代码优化3