Liuye Notebook
0%

编译原理-中间代码生成2

发表于 更新于 分类于 阅读次数： Valine：

阅读更多

1 简单赋值语句的翻译

赋值语句的基本文法

$$\begin{split} S &\to id = E; \\ E &\to E1 + E2 \\ E &\to E1 * E2 \\ E &\to -E1 \\ E &\to (E1) \\ E &\to id \end{split}$$

赋值语句翻译的主要任务：生成对表达式求值的三地址码

fig1

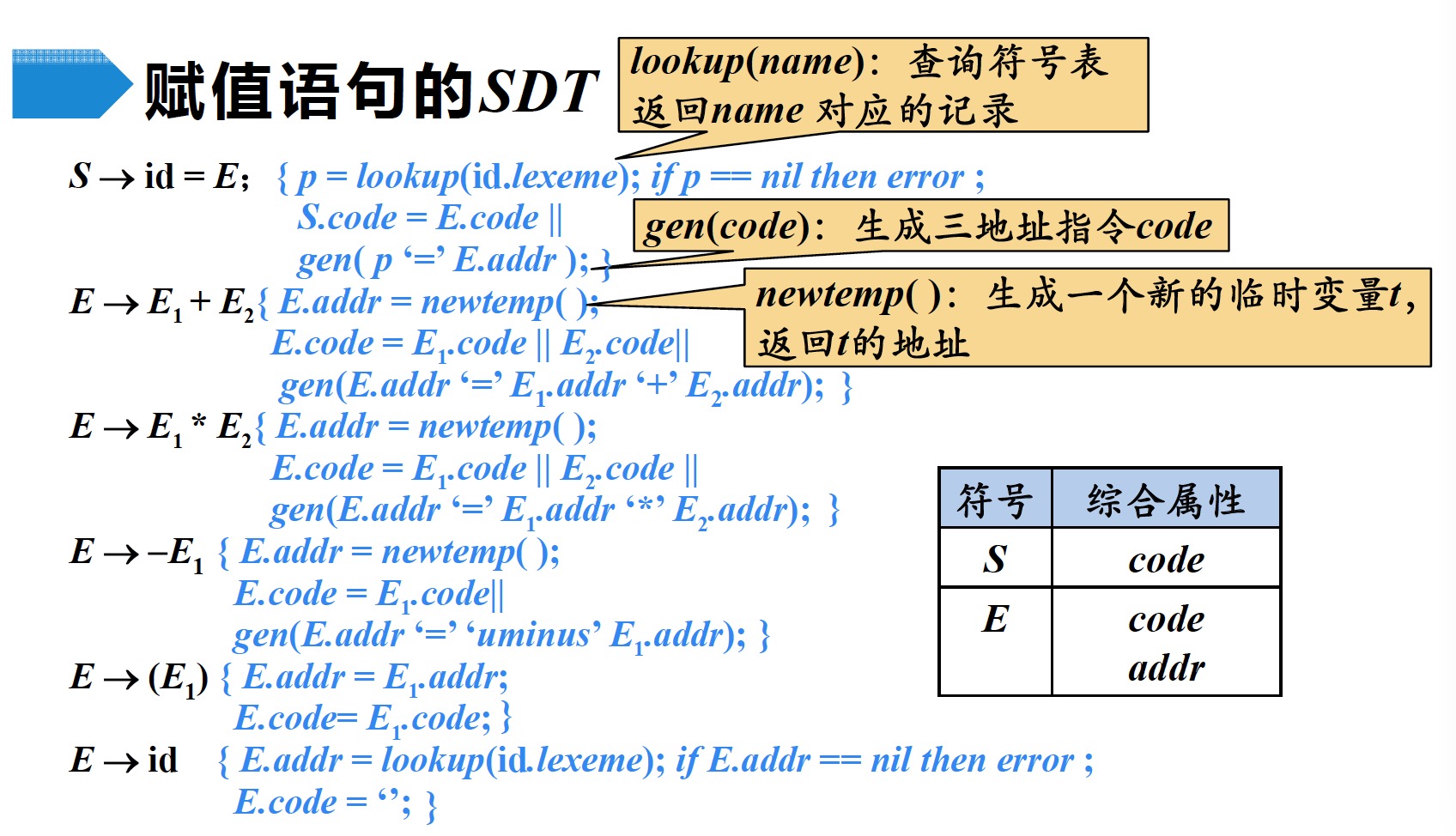
  • $lookup(name)$：查询符号表，返回name对应的记录
  • $gen(code)$：生成三地址指令
  • $newtemp()$：生成一个新的临时变量t，返回t的地址
  • ||：连接

在上述例子中，每个语义动作都得保留之前的所有code属性，即连接所有子表达式的code属性，因此得到的code指令序列可能会很长。因此采用增量的方式进行翻译。在增量方法中，$gen(code)$不仅要构造出一个新的三地址指令，还要将它添加。到至今为止已生成的指令序列之后

fig2

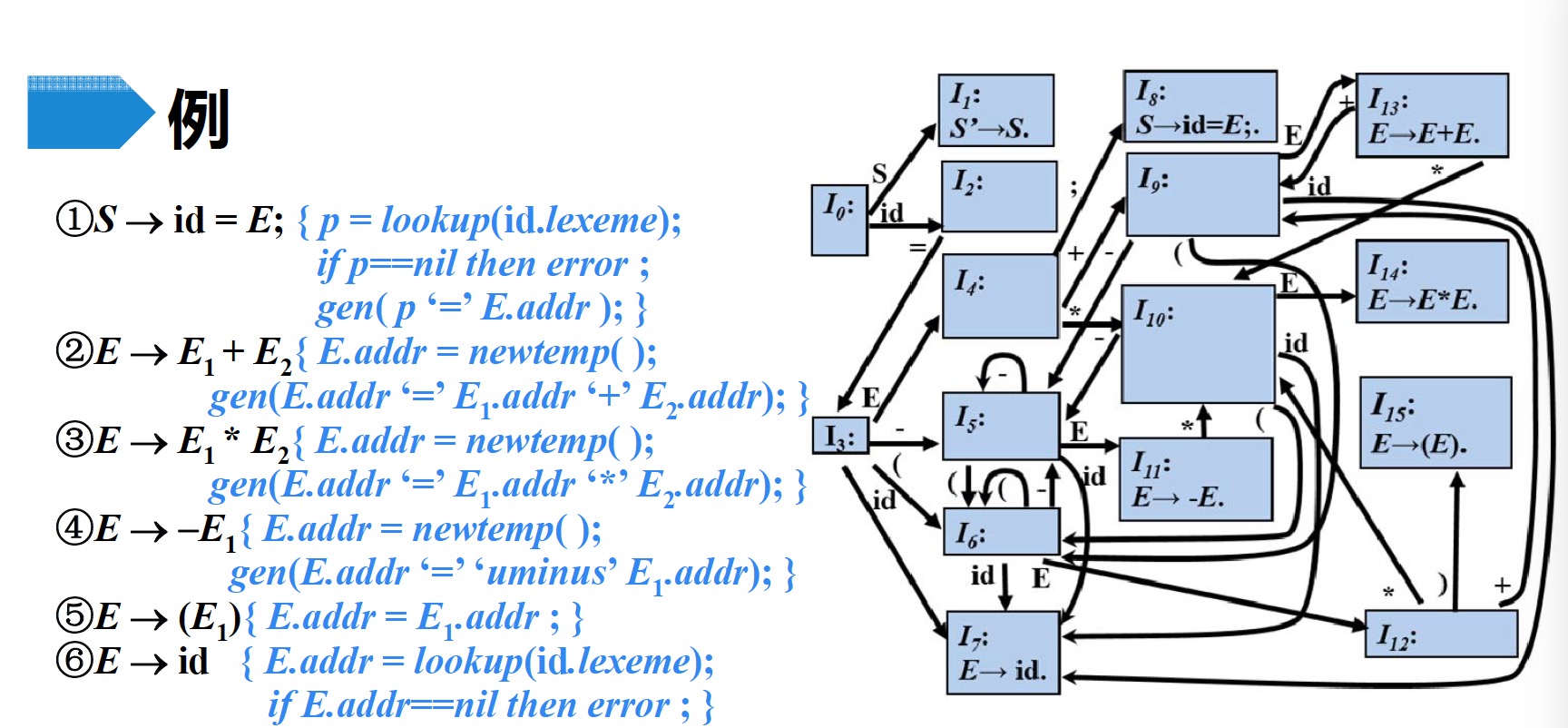
由于上述语法的产生式中，所有的语义动作都位于表达式末尾，因此可以采用自底向上的分析法，$LR$自动机如下图所示：

fig3

fig4

fig5

fig6

fig7

fig8

fig9

fig10

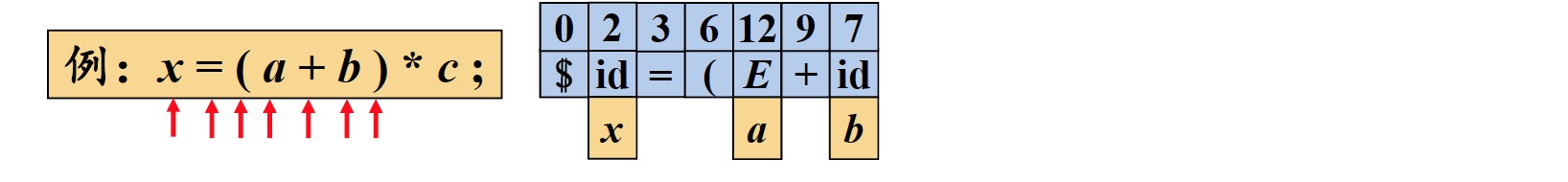
2 数组引用的翻译

赋值语句的基本文法

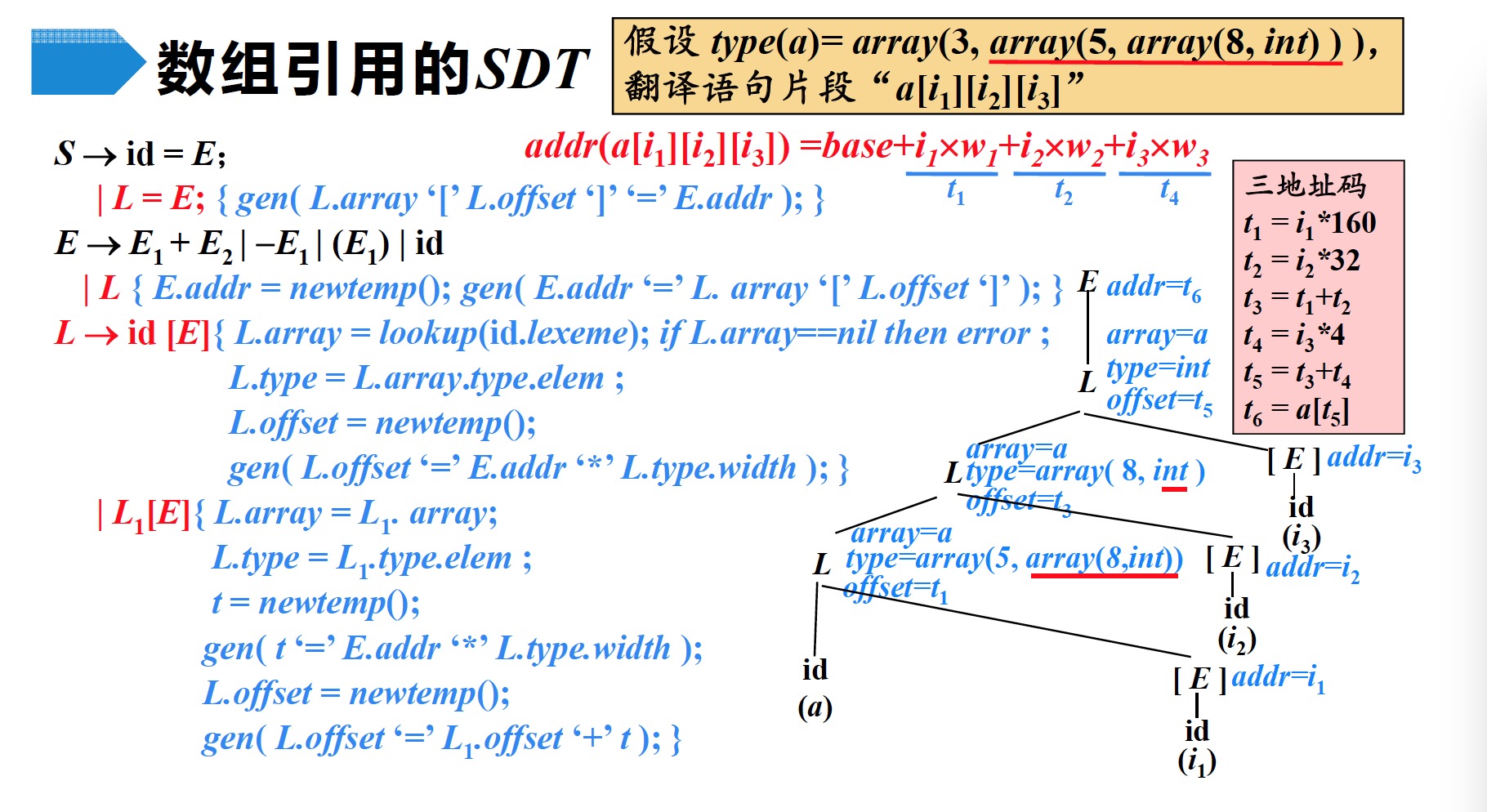
$$\begin{split} S &\to id = E; | L = E; \\ E &\to E_1 + E_2 | -E_1 | (E_1) | id | L \\ L &\to id [E] | L_1 [E] \\ \end{split}$$

将数组引用翻译成三地址码时要解决的主要问题是：确定数组元素的存放地址，也就是数组元素的寻址

2.1 数组元素寻址(Addressing Array Elements)

一维数组

  • 假设每个数组元素的宽度是$w$，则数组元素$a[i]$的相对地址是（其中，$base$是数组的基地址，$i \times w$是偏移地址）：
$$base + i \times w$$

二维数组

  • 假设一行的宽度是$w_1$，同一行中每个数组元素的宽度是$w_2$，则数组元素$a[i1][i2]$的相对地址是：
$$base + i_1 \times w_1 + i_2 \times w_2$$

k维数组

  • 数组元素$a[i_1][i_2]...[i_k]$的相对地址是：
$$\begin{split} base &+ i_1 \times w_1 + i_2 \times w_2 + ... + i_k \times w_k \\ w_1 &\to a[i_1] 的宽度 \\ w_2 &\to a[i_1][i_2] 的宽度 \\ &... \\ w_k &\to a[i_1][i_2]...[i_k]的宽度 \end{split}$$

2.2 数组元素赋值的翻译

需要为非终结符$L$增加以下综合属性

  • $L.type$：$L$生成的数组元素的类型
  • $L.offset$：指示一个临时变量，该临时变量用于累加公式中的$i_j \times w_j$项，从而计算数组引用的偏移量
  • $L.array$：数组名在符号表的入口地址

fig11

3 参考

  • 《MOOC-编译原理-陈鄞》