阅读更多
1 语法制导翻译方案SDT
语法制导翻译方案(SDT)是在产生式右部中嵌入了程序片段(称为语义动作)的CFG

SDT可以看作是SDD的具体实施方案
本节主要关注如何使用SDT来实现两类重要的SDD,因为在这两种情况下,SDT可在语法分析过程中实现
- 基本文法可以使用LR分析技术,且SDD是S属性的
- 基本文法可以使用LL分析技术,且SDD是L属性的
1.1 将S-SDD转换为SDT
将一个S-SDD转换为SDT的方法:将每个语义动作都放在产生式的最后
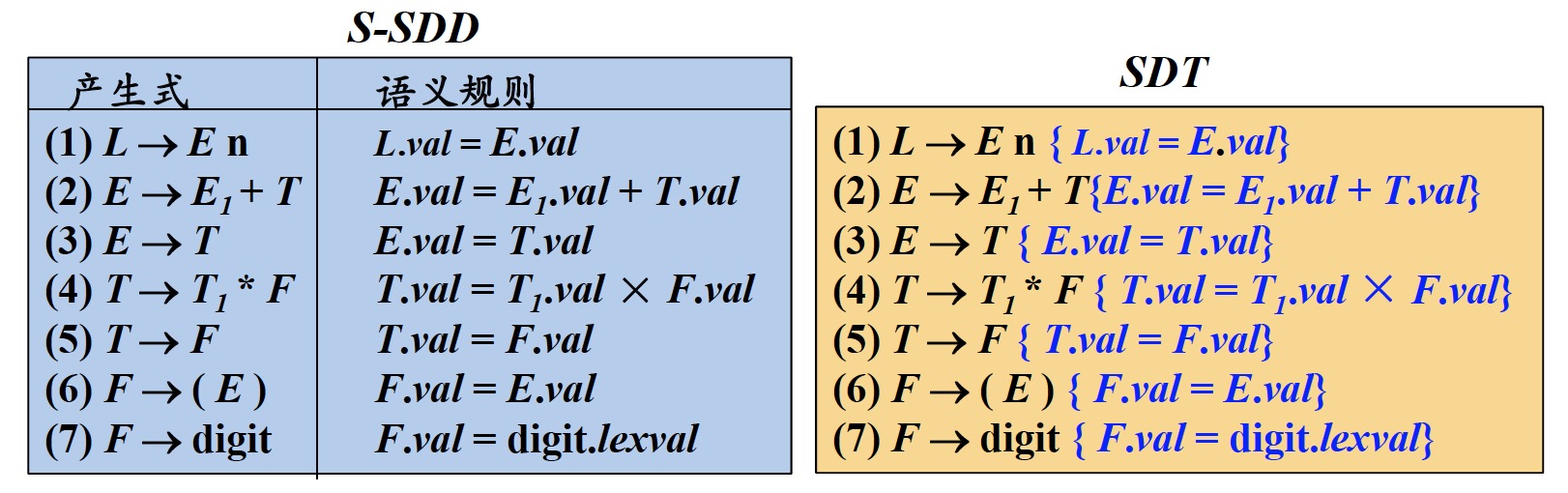
1.2 S-属性定义的SDT实现
如果一个S-SDD的基本文法可以使用LR分析技术,那么它的SDT可以在LR语法分析过程中实现
- 当归约发生时执行相应的语义动作
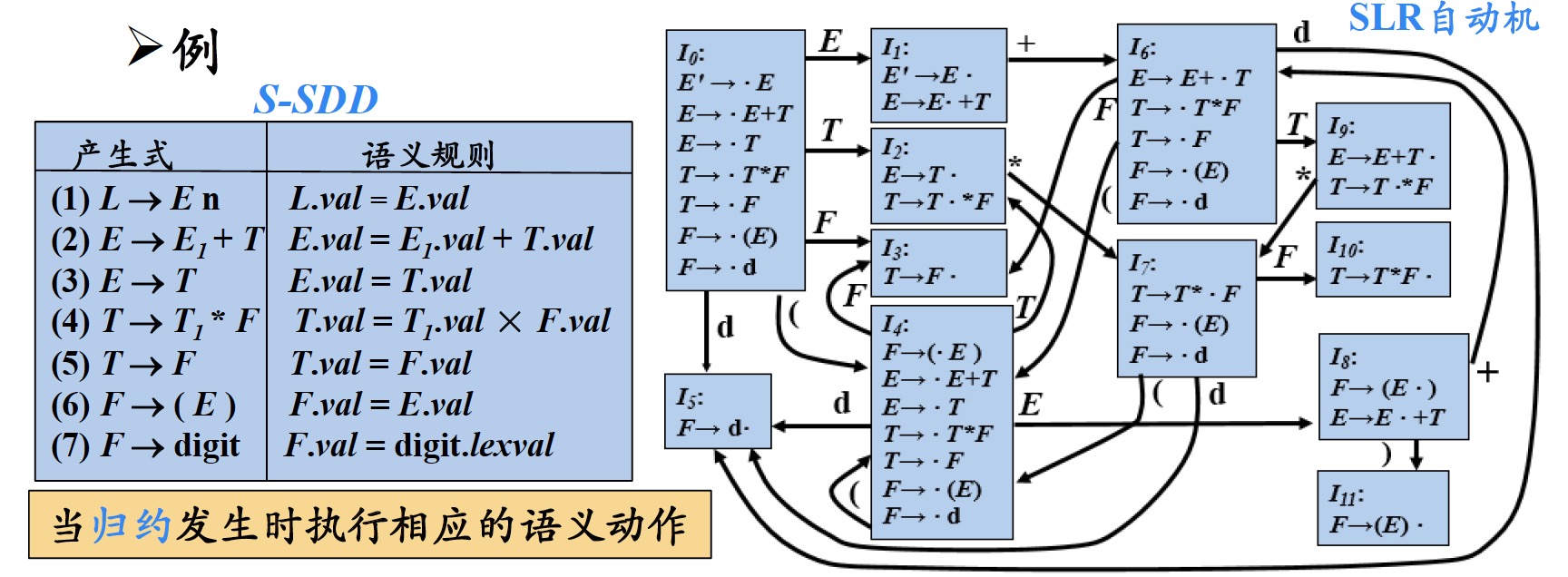
1.3 扩展的LR语法分析栈
在分析栈中使用一个附加的域来存放综合属性值。若支持多个属性,那么可以在栈中存放指针
此时,分析栈可以看成一个栈,栈元素包含状态、文法符号、综合属性三个域;分析栈也可以看成三个栈,分别是状态栈、文法符号栈、综合属性栈,分开看的理由是,入栈出栈并不完全同步
1.4 将语义动作中的抽象定义式改写成具体可执行的栈操作
即将语义翻译成相应的栈操作
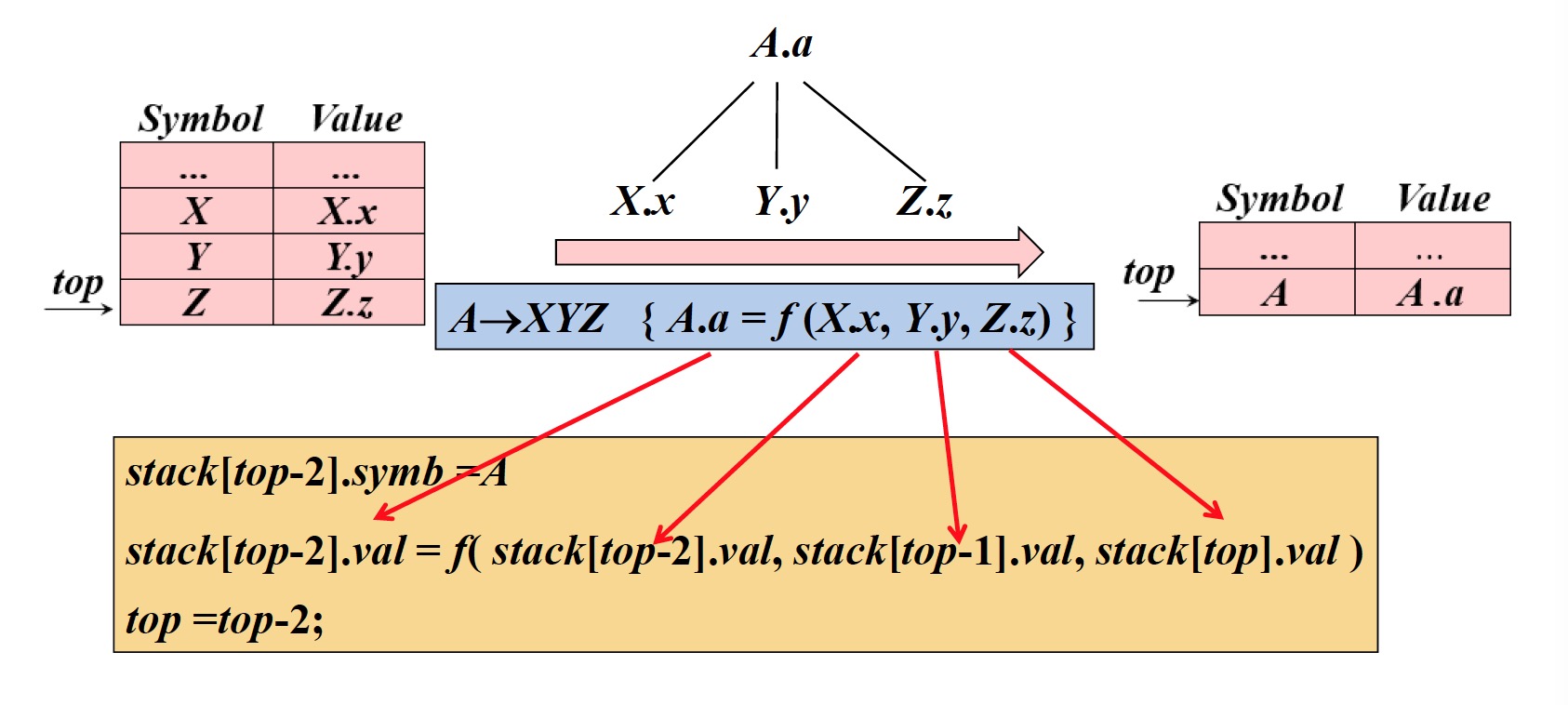
1.5 例:在自底向上语法分析栈中实现桌面计算器
桌面计算器的SDD定义如下:
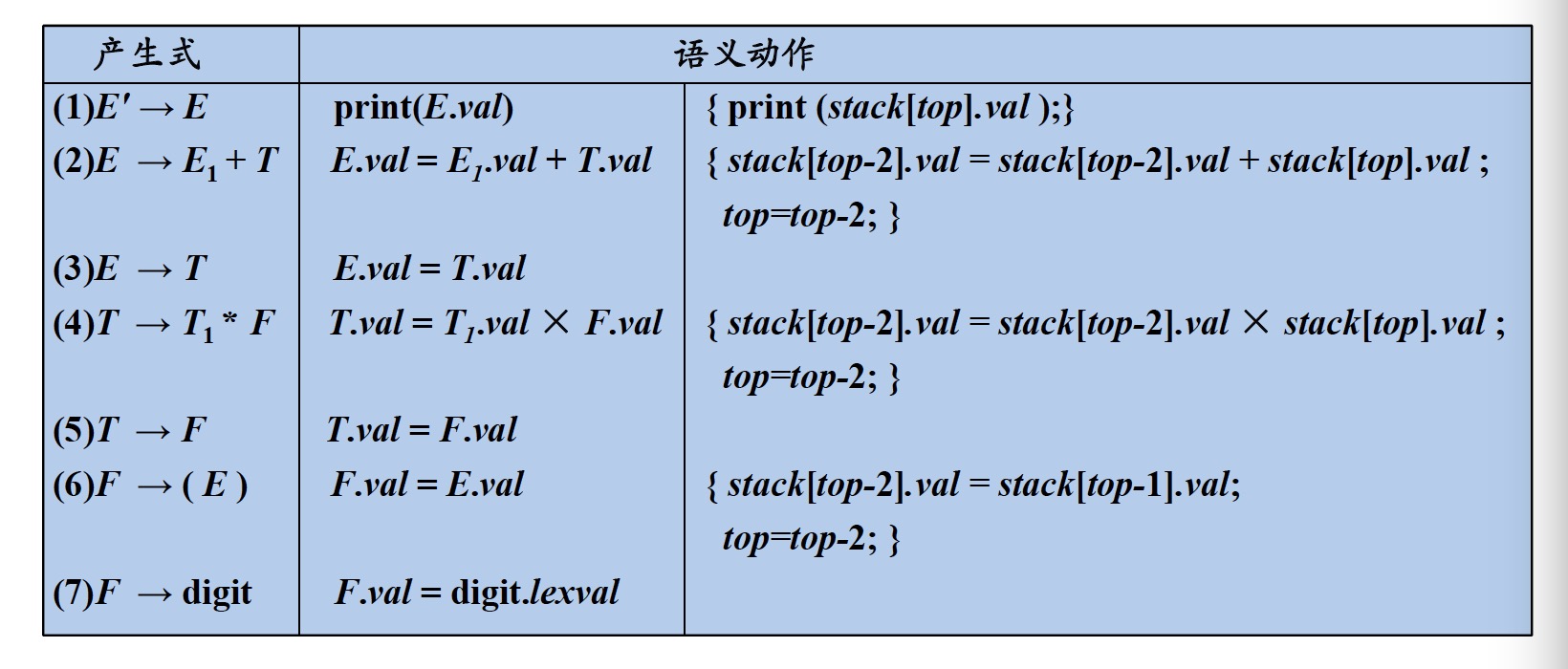
对应的SLR自动机如下:
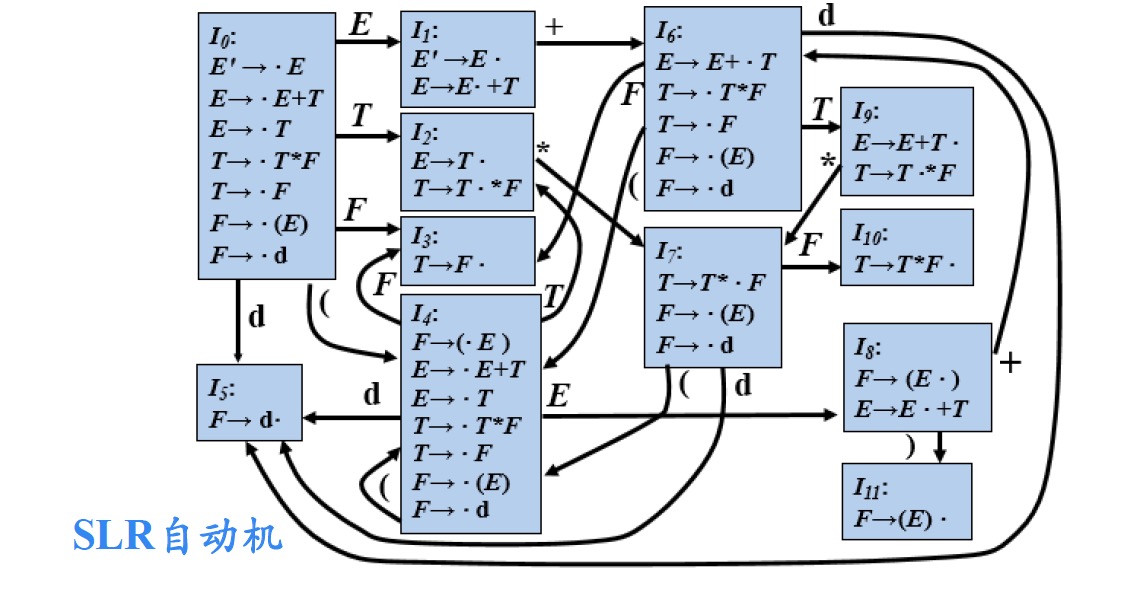
语法制导过程如下:
$$\begin{split} 状态栈&:0 \\ 符号栈&:\$ \\ 属性栈&:\_ \\ 剩余输入符号&:3\ast 5+4\$ \\ &\Downarrow \\ 输入符号d,&其属性值为3 \\ 状态栈&:0 \\ 符号栈&:\$,d \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 查表[0, d] = 5,&状态5进状态栈 \\ 状态栈&:0,5 \\ 符号栈&:\$,d \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 状态5遇到输入符号\ast时,根据第7个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号F \\ 状态栈&:0 \\ 符号栈&:\$,F \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 查表[0, F] = 3,&状态3进栈 \\ 状态栈&:0,3 \\ 符号栈&:\$,F \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 状态3遇到输入符号\ast时,根据第5个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号T \\ 状态栈&:0 \\ 符号栈&:\$,T \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 查表[0, T] = 2,&状态2进栈 \\ 状态栈&:0,2 \\ 符号栈&:\$,T \\ 属性栈&:\_,3 \\ 剩余输入符号&:\ast 5+4\$ \\ &\Downarrow \\ 输入符号\ast,&没有属性值 \\ 状态栈&:0,2 \\ 符号栈&:\$,T,\ast \\ 属性栈&:\_,3,\_ \\ 剩余输入符号&:5+4\$ \\ &\Downarrow \\ 查表[2, \ast] = 7,&状态7进栈 \\ 状态栈&:0,2,7 \\ 符号栈&:\$,T,\ast \\ 属性栈&:\_,3,\_ \\ 剩余输入符号&:5+4\$ \\ &\Downarrow \\ 输入符号d,&其属性值为5 状态栈&:0,2,7 \\ 符号栈&:\$,T,\ast,d \\ 属性栈&:\_,3,\_,5 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 查表[7, d] = 5,&状态5进栈 \\ 状态栈&:0,2,7,5 \\ 符号栈&:\$,T,\ast,d \\ 属性栈&:\_,3,\_,5 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 状态5遇到输入符号+时,根据第7个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号F \\ 状态栈&:0,2,7 \\ 符号栈&:\$,T,\ast,F \\ 属性栈&:\_,3,\_,5 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 查表[7, F] = 10,&状态10进栈 \\ 状态栈&:0,2,7,10 \\ 符号栈&:\$,T,\ast,F \\ 属性栈&:\_,3,\_,5 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 状态10遇到输入符号+时,根据第4个产生式进行归约,状态栈和符号栈出栈,&属性栈根据该产生式进行相应操作,并压入归约后的符号T \\ 状态栈&:0 \\ 符号栈&:\$,T \\ 属性栈&:\_,15 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 查表[0, T] = 2,&状态2进栈 \\ 状态栈&:0,2 \\ 符号栈&:\$,T \\ 属性栈&:\_,15 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 状态2遇到输入符号+时,根据第3个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号E \\ 状态栈&:0 \\ 符号栈&:\$,E \\ 属性栈&:\_,15 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 查表[0, E] = 1,&状态1进栈 \\ 状态栈&:0,1 \\ 符号栈&:\$,E \\ 属性栈&:\_,15 \\ 剩余输入符号&:+4\$ \\ &\Downarrow \\ 输入符号+,&没有属性值 \\ 状态栈&:0,1 \\ 符号栈&:\$,E,+ \\ 属性栈&:\_,15,\_ \\ 剩余输入符号&:4\$ \\ &\Downarrow \\ 查表[1, +] = 6,&状态6进栈 \\ 状态栈&:0,1,6 \\ 符号栈&:\$,E,+ \\ 属性栈&:\_,15,\_ \\ 剩余输入符号&:4\$ \\ &\Downarrow \\ 输入符号d,&其属性值为4 \\ 状态栈&:0,1,6 \\ 符号栈&:\$,E,+,d \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 查表[6, d] = 5,&状态5进栈 \\ 状态栈&:0,1,6,5 \\ 符号栈&:\$,E,+,d \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 状态5遇到输入符号\$时,根据第7个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号F \\ 状态栈&:0,1,6 \\ 符号栈&:\$,E,+,F \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 查表[6, F] = 4,&状态3进栈 \\ 状态栈&:0,1,6,3 \\ 符号栈&:\$,E,+,F \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 状态3遇到输入符号\$时,根据第5个产生式进行归约,&状态栈和符号栈出栈,属性栈不变,并压入归约后的符号T \\ 状态栈&:0,1,6 \\ 符号栈&:\$,E,+,T \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 查表[6, T] = 9,&状态9进栈 \\ 状态栈&:0,1,6,9 \\ 符号栈&:\$,E,+,T \\ 属性栈&:\_,15,\_,4 \\ 剩余输入符号&:\$ \\ &\Downarrow \\ 状态9遇到输入符号\$时,根据第2个产生式进行归约,&状态栈和符号栈出栈,属性栈根据该产生式进行相应操作,并压入归约后的符号E \\ 状态栈&:0 \\ 符号栈&:\$,E \\ 属性栈&:\_,19 \\ 剩余输入符号&:\$ \\ 查表[0, E] = 1,&状态1进栈 \\ 状态栈&:0,1 \\ 符号栈&:\$,E \\ 属性栈&:\_,19 \\ 剩余输入符号&:\$ \\ 状态1遇到\$时,&成功接收 \end{split}$$1.6 将L-SDD转换为SDT
将L-SDD转换为SDT的规则
- 将计算某个非终结符号A的继承属性的动作插入到产生式右部中紧靠在A的本次出现之前的位置上
- 将计算一个产生式左部符号的综合属性的动作放置在这个产生式右部的最右端

1.7 L-属性定义的SDT实现
如果一个L-SDD的基本文法可以使用LL分析技术,那么它的SDT可以在LL或LR语法分析过程中实现
- 在非递归的预测分析过程中进行语义翻译
- 在递归的预测分析过程中进行语义翻译
- 在LR分析过程中进行语义翻译
2 在非递归的预测分析过程中进行翻译
2.1 扩展语法分析栈
此时语法分析栈中包含三种类型的元素
- $action$:用于放置指向将被执行的语义动作代码的指针
- $A$:用于放置$A$的继承属性(继承属性与非终结符放在一起)
- $Asyn$:用于放置$A$的综合属性(综合属性与非终结符分开存放)
2.2 分析过程详解
SDD定义如下

输入符号:3 * 5
- 初始时,仅有非终结符$T$,且带有综合属性

- 输入指针指向输入符号3,根据产生式1替换栈顶元素$T$
- 弹出栈顶元素$T$
- 其中$F$和$T^{\prime}$分别带有综合属性,因此总共入栈元素共有6项

- 输入指针指向输入符号3,根据产生式4替换栈顶元素$F$
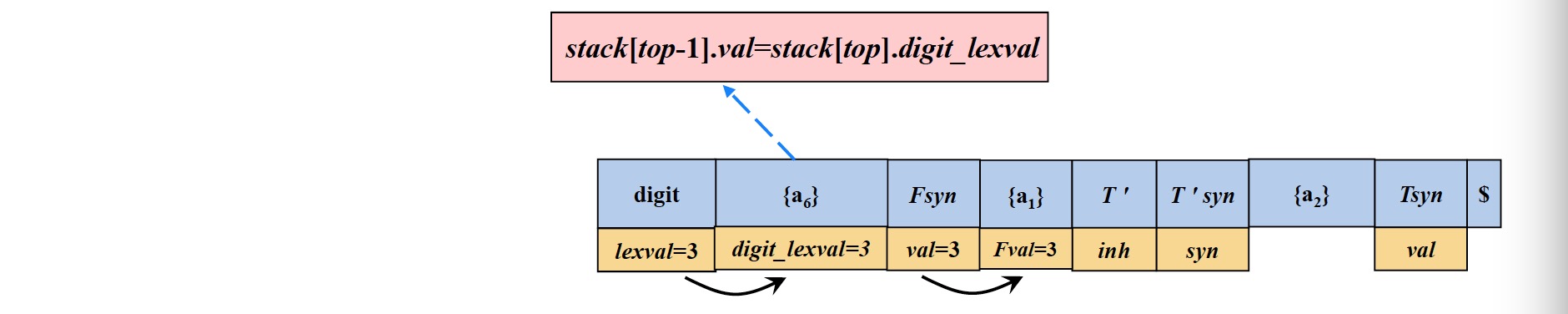
- 输入指针指向输入符号3,与栈顶元素$digit$匹配成功,输入指针向前移动一位
- $digit$元素出栈,在$digit$元素出栈之前,需要将结果保存在$\{ a_6 \}$中(因为$a_6$定义的操作需要用到该$digit$元素的值)
- 根据$a_6$定义的操作,计算$F$的综合属性(保存在$Fsyn$中),然后动作属性$\{ a_6 \}$出栈
- $Fsyn$元素出栈,在$Fsyn$元素出栈之前,需要将结果保存在$\{ a_1 \}$中(因为$a_1$定义的操作需要用到$Fsyn$的值)
- 根据$a_1$定义的操作,计算$T^{\prime}$的继承属性(保存在$T^{\prime}$中),然后动作属性$\{ a_1 \}$出栈
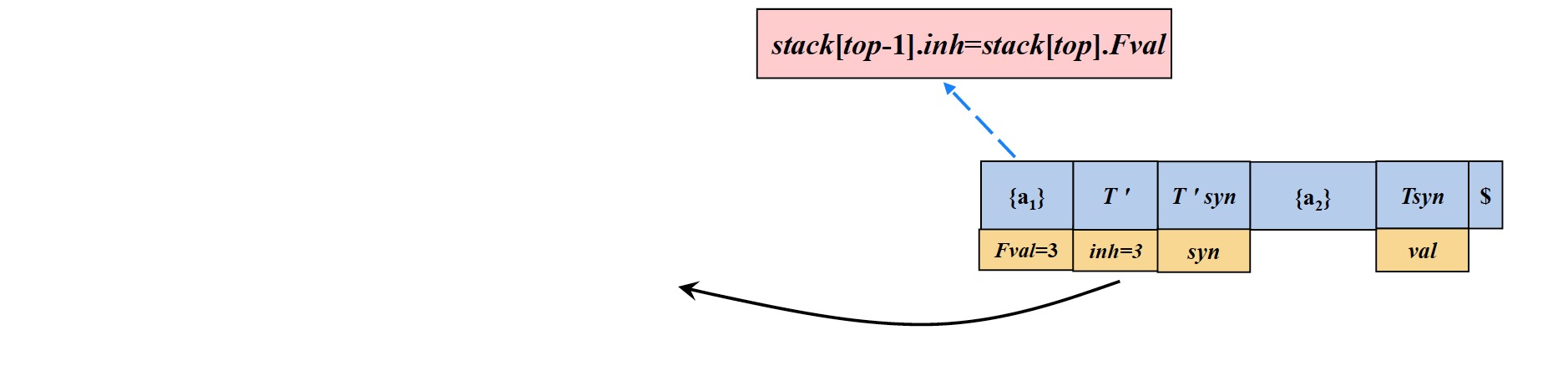
- 输入指针指向输入符号*,根据产生式2替换栈顶元素$T^{\prime}$,由于$T_1^{\prime}$的继承属性依赖$T^{\prime}$的继承属性,因此在$T^{\prime}$元素出栈之前,要将$T^{\prime}$的继承属性保存到$\{ a_3 \}$中

- 输入指针指向输入符号*,与栈顶元素*匹配成功,输入指针先前移动一位,栈顶元素出栈
- 输入指针指向输入符号5,根据产生式4替换栈顶元素$F$
- 输入指针指向输入符号5,与栈顶元素$digit$匹配成功,输入指针向前移动一位
- $digit$元素出栈,在$digit$元素出栈之前,需要将结果保存在$\{ a_6 \}$中(因为$a_6$定义的操作需要用到该$digit$元素的值)
- 根据$a_6$定义的操作,计算$F$的综合属性(保存在$Fsyn$中),然后动作属性$\{ a_6 \}$出栈
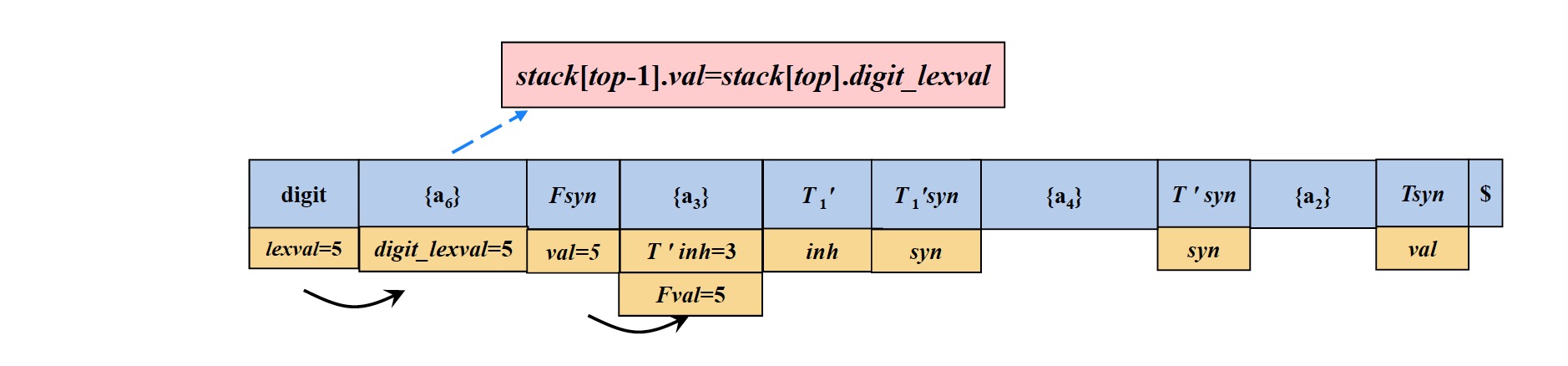
- $Fsyn$元素出栈,在$Fsyn$元素出栈之前,需要将结果保存在$\{ a_3 \}$(因为$a_3$定义的操作需要用到该$Fsyn$元素的值)
- 执行$a_3$定义的操作,计算$T_1^{\prime}$的继承属性(保存在$T_1^{\prime}$中),然后动作属性$\{ a_3 \}$出栈
- 输入指针指向输入符号$\$$,根据产生式3替换栈顶元素$T_1^{\prime}$,且将$T_1^{\prime}$的值保存在$\{ a_5 \}$中(因为$a_5$定义的操作需要用到该$T_1^{\prime}$元素的值)

- 执行$a_5$定义的操作,计算$T_1^{\prime}$的综合属性(保存在$T_1^{\prime}syn$中),然后动作属性$\{ a_5 \}$出栈
- $T_1^{\prime}syn$元素出栈,在$T_1^{\prime}syn$元素出栈之前,将其保存在$\{ a_4 \}$中(因为$a_4$定义的操作需要用到该$T_1^{\prime}syn$元素的值)
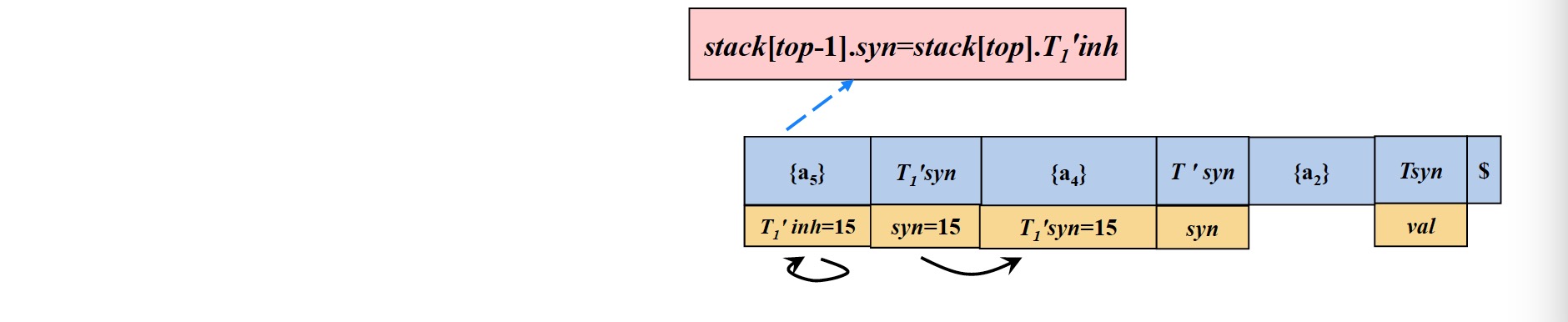
- 执行$a_4$定义的操作,计算$T^{\prime}$的综合属性(保存在$T^{\prime}syn$中),然后动作属性$\{ a_4 \}$出栈
- $T^{\prime}syn$元素出栈,在$T^{\prime}syn$元素出栈之前,将其保存在$\{ a_2 \}$中(因为$a_2$定义的操作需要用到该$T^{\prime}syn$元素的值)
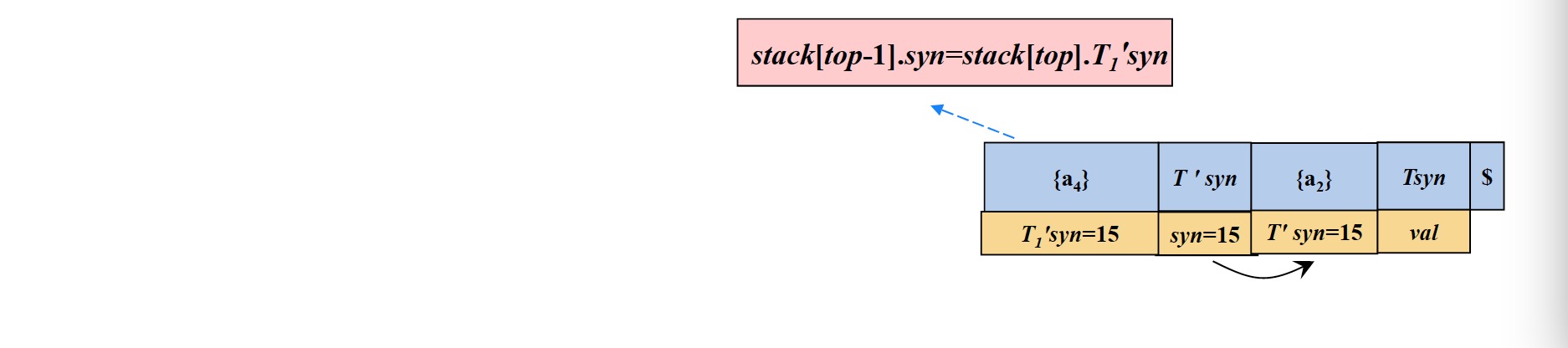
- 执行$a_2$定义的操作,计算文法开始符号$T$的综合属性值(保存在$Tsyn$中),然后动作属性$\{ a_2 \}$出栈
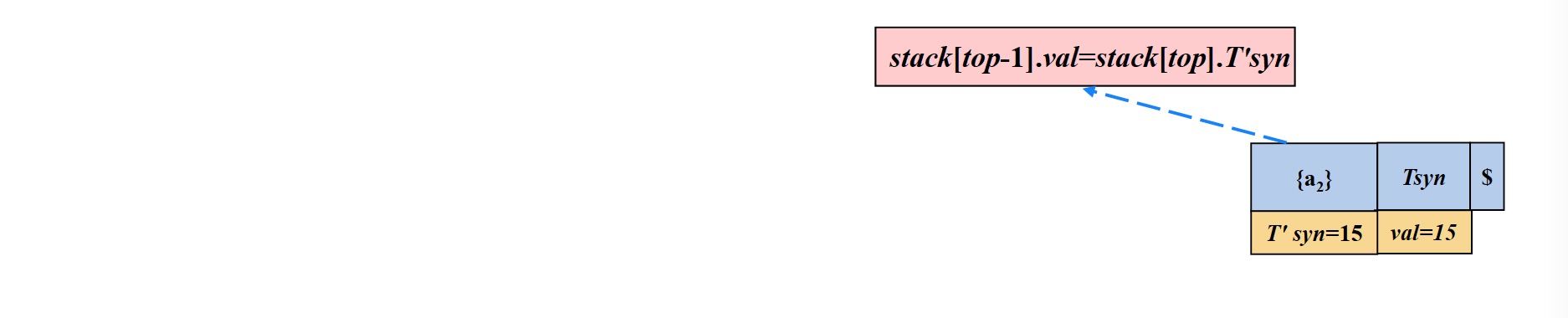
2.3 分析栈中的每一个记录都对应着一段执行代码
综合记录出栈时,要将综合属性值复制给后面特定的语义动作
变量展开时(即变量本身的记录出栈时),如果其含有继承属性,则要将继承属性值复制给后面特定的语义动作




3 参考
- 《MOOC-编译原理-陈鄞》