阅读更多
1 $SLR$分析
$SLR$(Simple)分析法的基本思想如下图所示
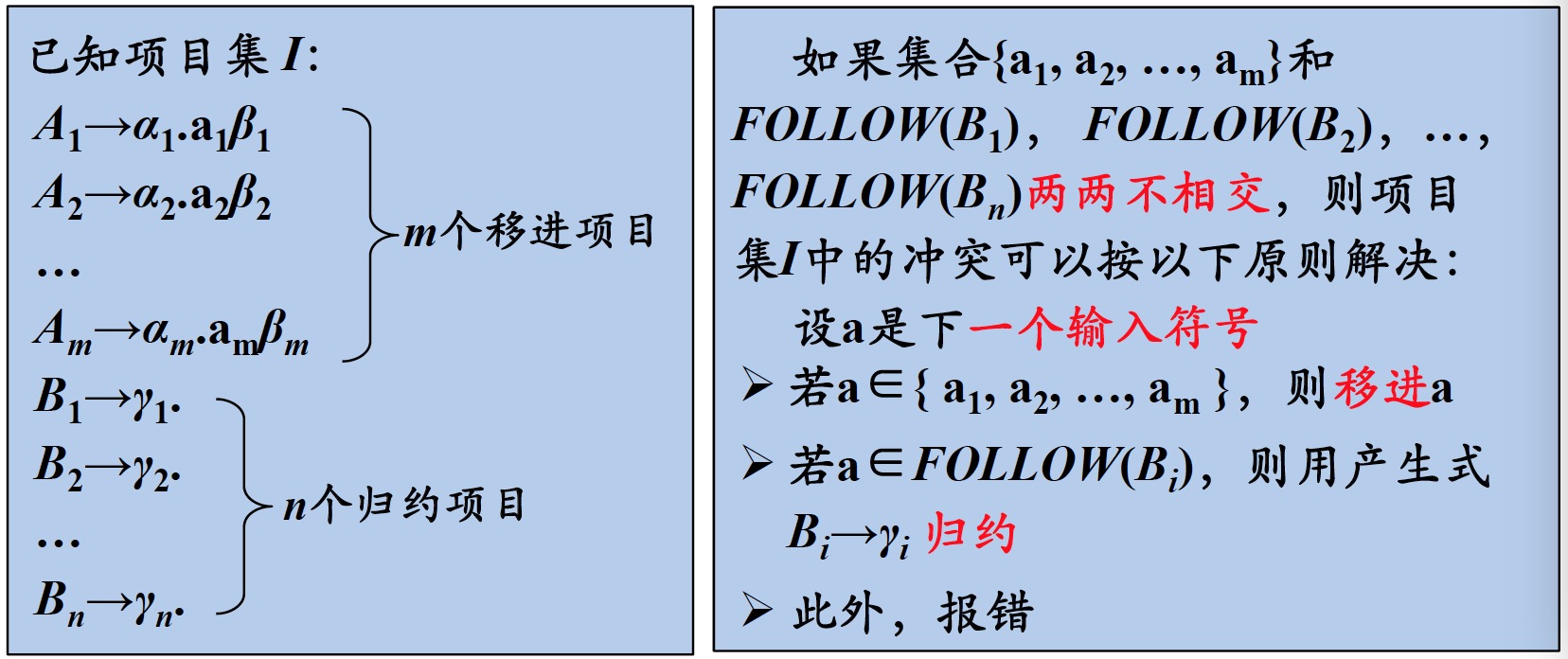
其中,$SLR$分析表与$LR(0)$分析表的区别
- $LR(0)$分析表归约状态,遇到任何输入符号都采取归约动作
- $SLR$分析表归约状态,遇到位于$FOLLOW$集中的符号才采取归约动作
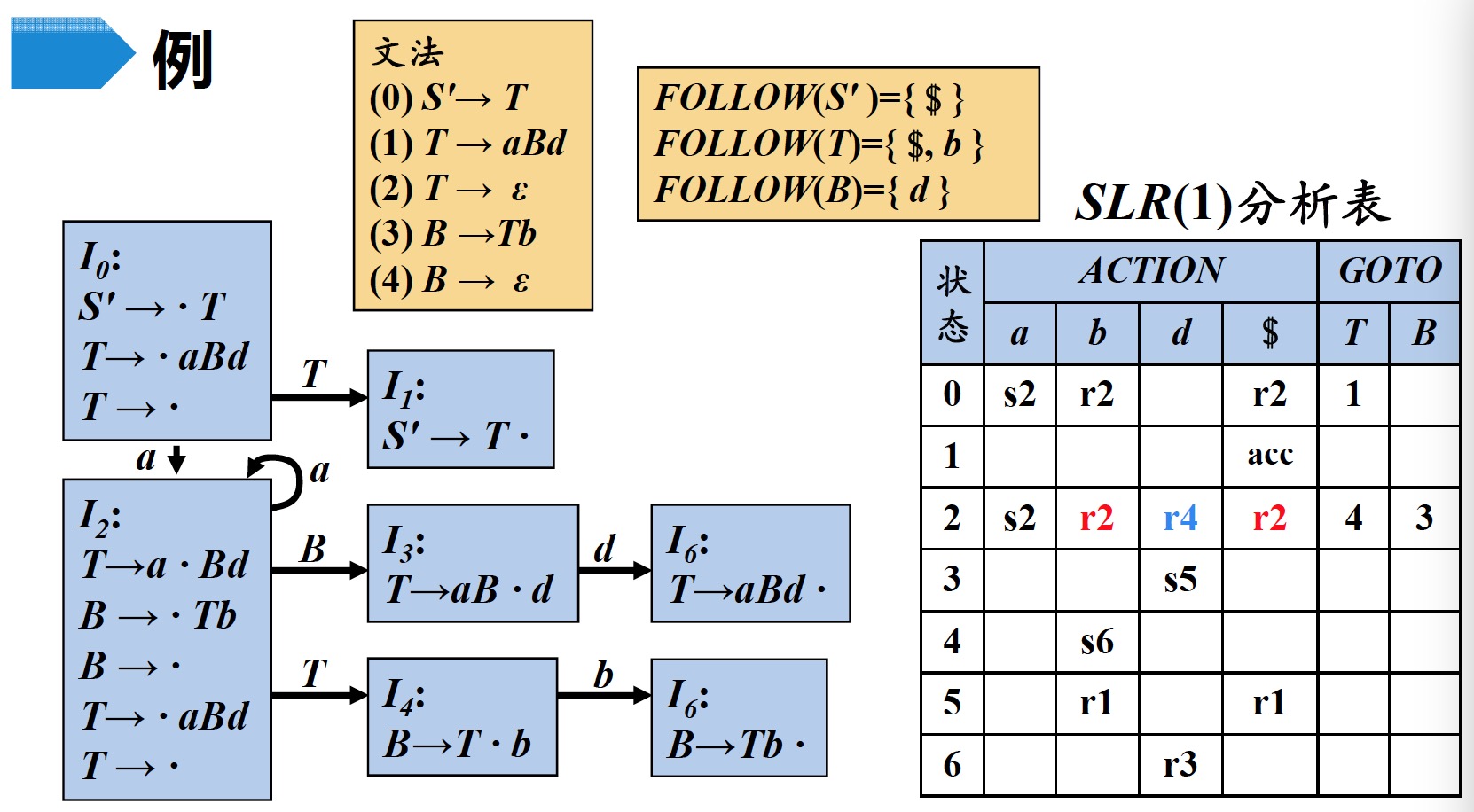
1.1 $SLR$分析表构造算法
- 构造$G^{\prime}$的规范$LR(0)$项集族$C = \{ I_0, I_1,... , I_n \}$
- 令$I_i$对应状态$i$。状态$i$的语法分析动作按照下面的方法决定:
- $\textbf{if}\; A \to \alpha \cdot a \beta \in I_i \;\textbf{and}\; GOTO(I_i, a) = I_j \;\textbf{then}\; ACTION[i, a] = sj$
- $\textbf{if}\; A \to \alpha \cdot B \beta \in I_i \;\textbf{and}\; GOTO(I_i, B) = I_j \;\textbf{then}\; GOTO[i, B] = j$
- $\textbf{if}\; A \to \alpha \cdot \in I_i 且 A \ne S^{\prime} \;\textbf{then}\; \;\textbf{for}\; \forall a \in FOLLOW(A) \;\textbf{do}\; ACTION[i, a] = rj$($j$是产生式$A \to \alpha$的编号)(与$LR(0)$分析表算法的唯一区别)
- $\textbf{if}\; S^{\prime} \to S \cdot \in I_i \;\textbf{then}\; ACTION [ i,\$] = acc$
- 没有定义的所有条目都设置为“error”
如果给定文法的$SLR$分析表中不存在有冲突的动作,那么该文法称为$SLR$文法
1.2 $SLR$分析中的冲突
可能产生移进/归约冲突,如下图所示
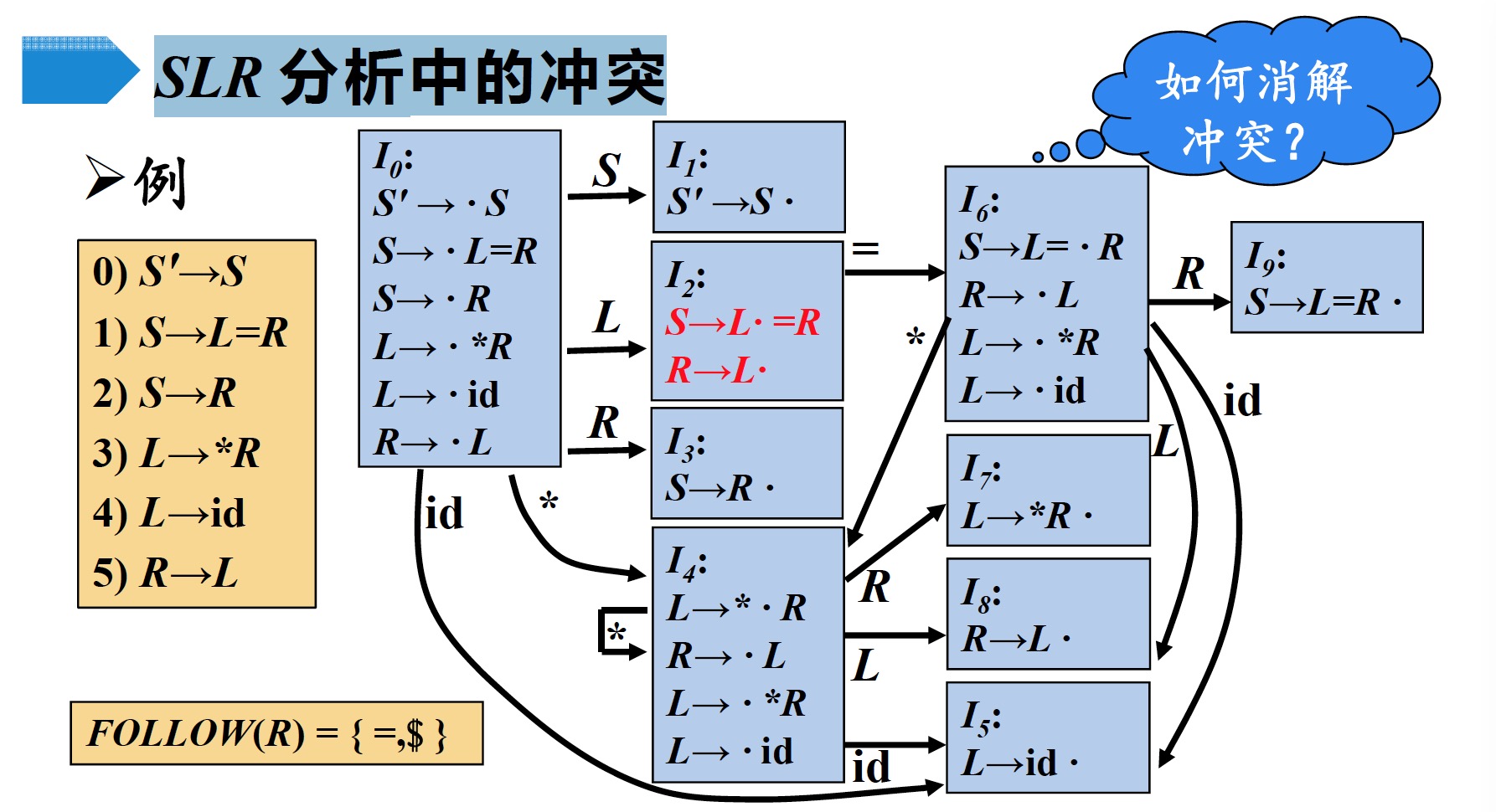
如上图所示,对于状态$I_2$会产生如下冲突
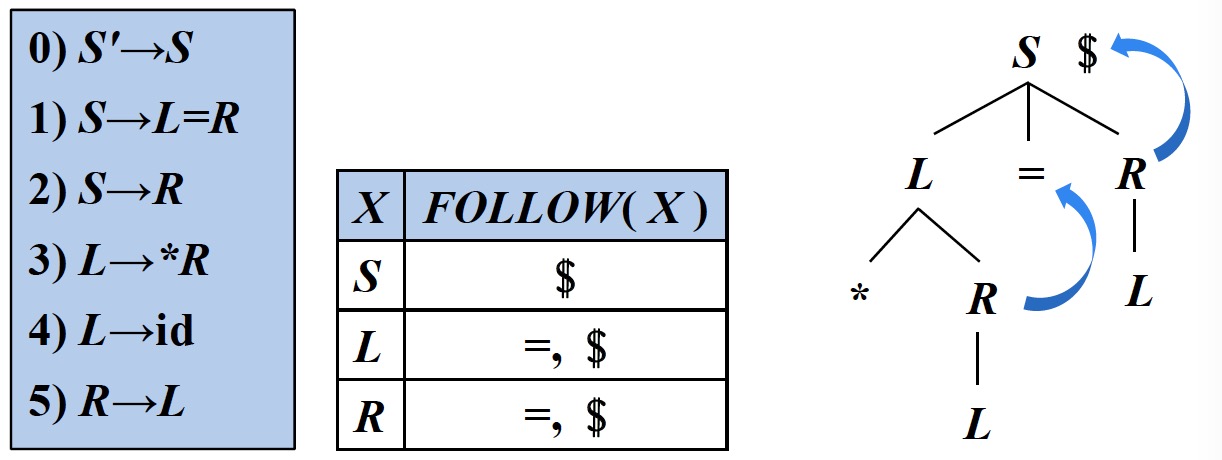
- $S \to L \;\cdot = R\;\;$表示当下一个符号是$=$时,采取移入动作
- $R \to L \cdot\;\;$表示当下一个符号是$=$或$\$$时,采取归约动作
2 $LR(1)$分析法
2.1 $LR(1)$分析法的提出
$SLR$分析存在的问题
- $SLR$只是简单地考察下一个输入符号$b$是否属于与归约项目$A \to \alpha$相关联的$FOLLOW(A)$,但$b \in FOLLOW(A)$只是归约$\alpha$的一个必要条件,而非充分条件
- 对于产生式$A \to \alpha$的归约,在不同使用位置,$A$会要求不同的后继符号
- 在特定位置,$A$的后继符集合是$FOLLOW(A)$的子集,一般情况下是真子集(例如上图中,非终结符$R$的后继符一个是$=$,另一个是$\$$,而$FOLLOW(R) = \{ =, \$ \}$)
2.2 规范$LR(1)$项目
将一般形式为$[A \to \alpha \cdot \beta, a]$的项称为$LR(1)$项,其中$A \to \alpha \beta$是一个产生式,$a$是一个终结符(这里将$\$$视为一个特殊的终结符)。它表示在当前状态下,$A$后面必须紧跟的终结符,称为该项的展望符(lookahead)
- $LR(1)$中的1指的是项的第二个分量的长度
- 在形如$[A \to \alpha \cdot \beta, a]$且$\beta \ne \varepsilon$的项中,展望符$a$没有任何作用(即对于移入项目,展望符是没有作用的)
- 但是一个形如$[A \to \alpha \cdot, a]$的项在只有在下一个输入符号等于$a$时才可以按照$A \to \alpha$进行归约
- 这样的a的集合总是$FOLLOW(A)$的子集,而且它通常是一个真子集
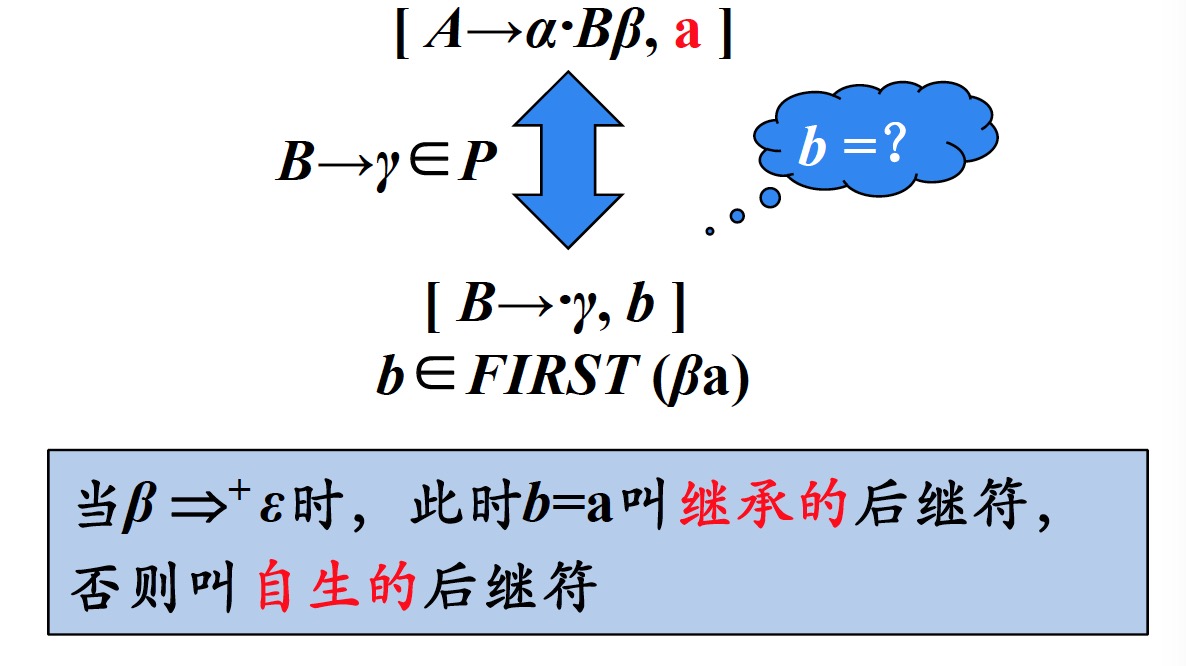
2.3 等价$LR(1)$项目
2.4 例子
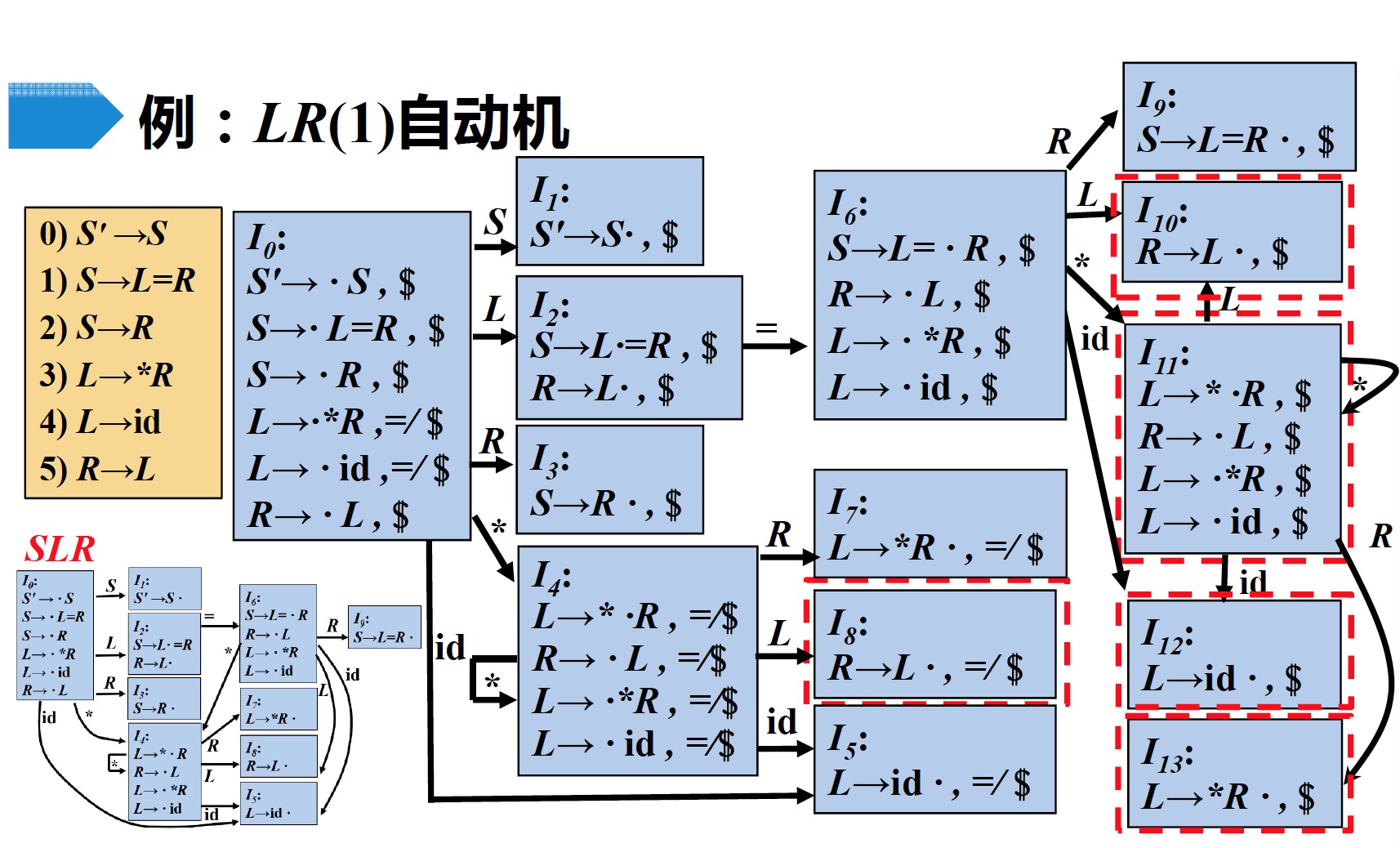
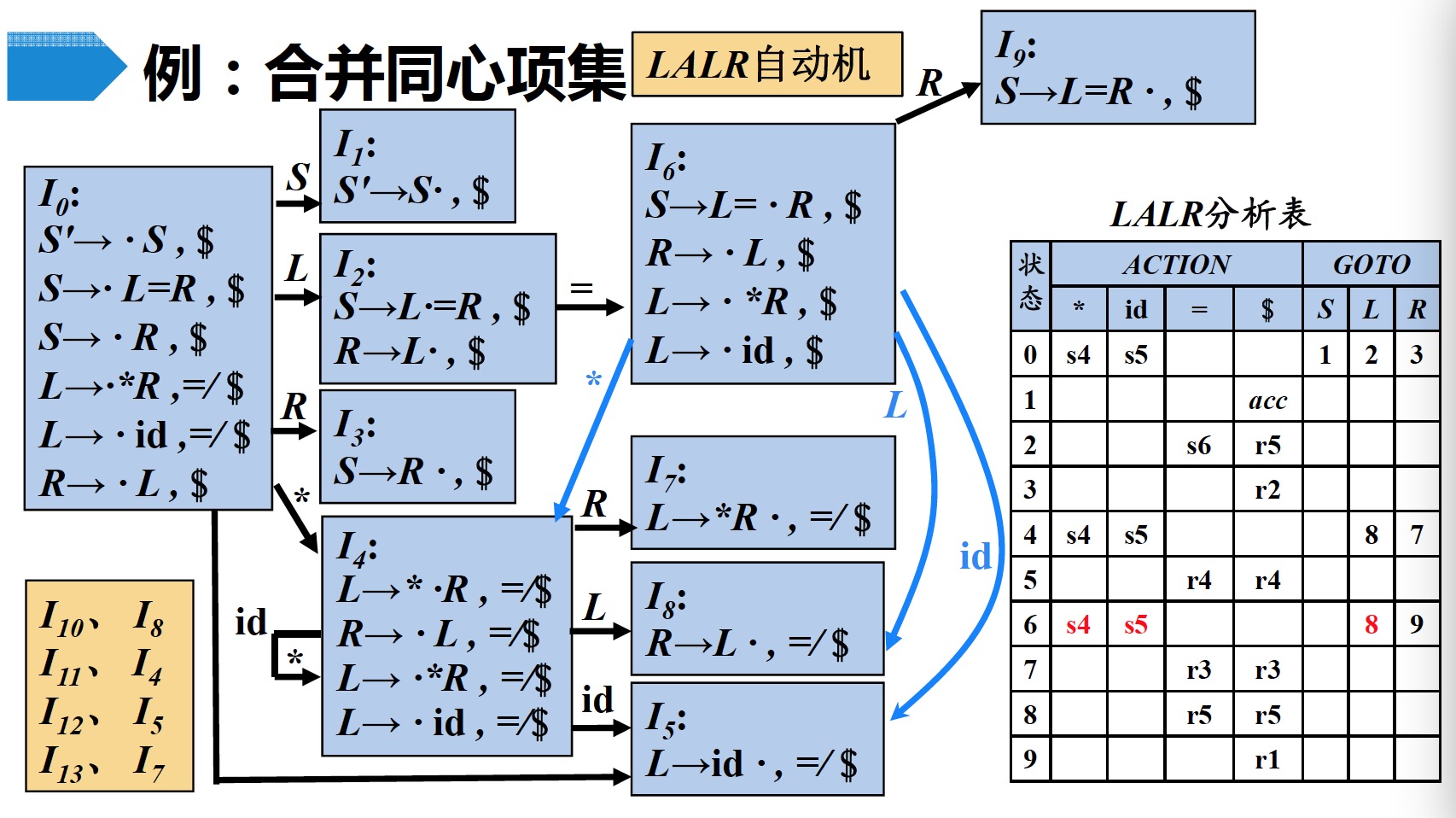
可以看出,该文法的$SLR$自动机与$LR(1)$自动机的差别就是多了右边的几个状态,而且以下几对状态是同心的(如果除展望符外,两个$LR(1)$项目集是相同的,则称这两个$LR(1)$项目集是同心的)
- $I_{10}与I_8$
- $I_{11}与I_4$
- $I_{12}与I_5$
- $I_{13}与I_7$
2.5 $LR(1)$项目集闭包
$$CLOSURE(I) = I \cup \{ [B \to \cdot \gamma, b] | [A \to \alpha \cdot B \beta, a] ∈ CLOSURE(I), B \to \gamma \in P, b \in FIRST(\beta a) \}$$
2.6 $GOTO$函数
$$GOTO(I, X) = CLOSURE( \{ [A \to \alpha X \cdot \beta, a]|[A \to \alpha \cdot X \beta, a] \in I \} )$$
2.7 为文法$G^{\prime}$构造$LR(1)$项集族

2.8 $LR(1)$自动机的形式化定义
文法
$$G = ( V_N, V_T, P, S )$$$LR(1)$自动机
$$M = ( C, V_N \cup V_T, GOTO, I_0, F )$$- $C = \{I_0 \} \cup \{ I | \exists J \in C, X \in V_N \cup V_T, I = GOTO(J,X) \}$
- $I_0 = CLOSURE(\{ S^{\prime} \to \cdot S, \$ \})$
- $F = \{ CLOSURE(\{ S^{\prime} \to S \cdot, \$ \}) \}$
2.9 $LR(1)$分析表构造算法
- 构造$G^{\prime}$的规范$LR(1)$项集族$C = \{ I_0, I_1,... , I_n \}$
- 根据$I_i$构造状态$i$。状态$i$的语法分析动作按照下面的方法决定:
- $\textbf{if}\; [A \to \alpha \cdot a \beta, b] \in I_i \;\textbf{and}\; GOTO(I_i, a) = I_j \;\textbf{then}\; ACTION[i, a] = sj$
- $\textbf{if}\; [A \to \alpha \cdot B \beta, b] \in I_i \;\textbf{and}\; GOTO(I_i, B) = I_j \;\textbf{then}\; GOTO[i, B] = j$
- $\textbf{if}\; [A \to \alpha \cdot, a] \in I_i 且 A \ne S^{\prime} \;\textbf{then}\; ACTION[i, a] = rj$($j$是产生式$A \to \alpha$的编号)
- $\textbf{if}\; [S^{\prime} \to S \cdot, \$] \in I_i \;\textbf{then}\; ACTION [ i,\$] = acc$
- 没有定义的所有条目都设置为“error”
如果$LR(1)$分析表中没有语法分析动作冲突,那么给定的文法就称为$LR(1)$文法
3 $LALR$分析法
3.1 $LALR$分析法的提出
首先,$LR(1)$分析法会产生许多同心状态,如下图中红色标注之处
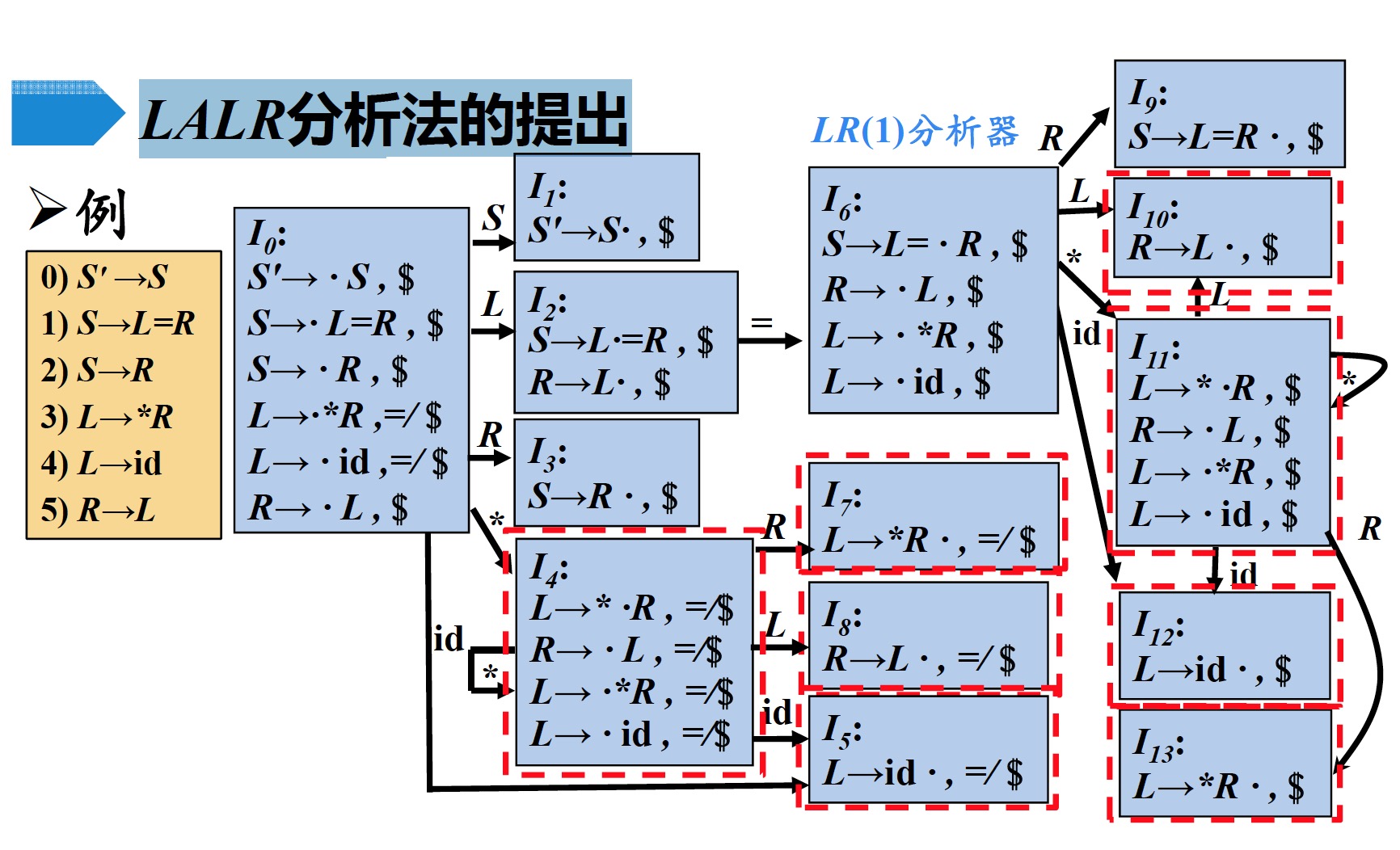
3.2 $LALR(lookahead-LR)$分析的基本思想
- 寻找具有相同核心的$LR(1)$项集,并将这些项集合并为一个项集。所谓项集的核心就是其第一分量的集合
- 合并后的展望符集合仍为$FOLLOW$集的子集
- 然后根据合并后得到的项集族构造语法分析表
- 如果分析表中没有语法分析动作冲突,给定的文法就称为$LALR(1)$文法,就可以根据该分析表进行语法分析
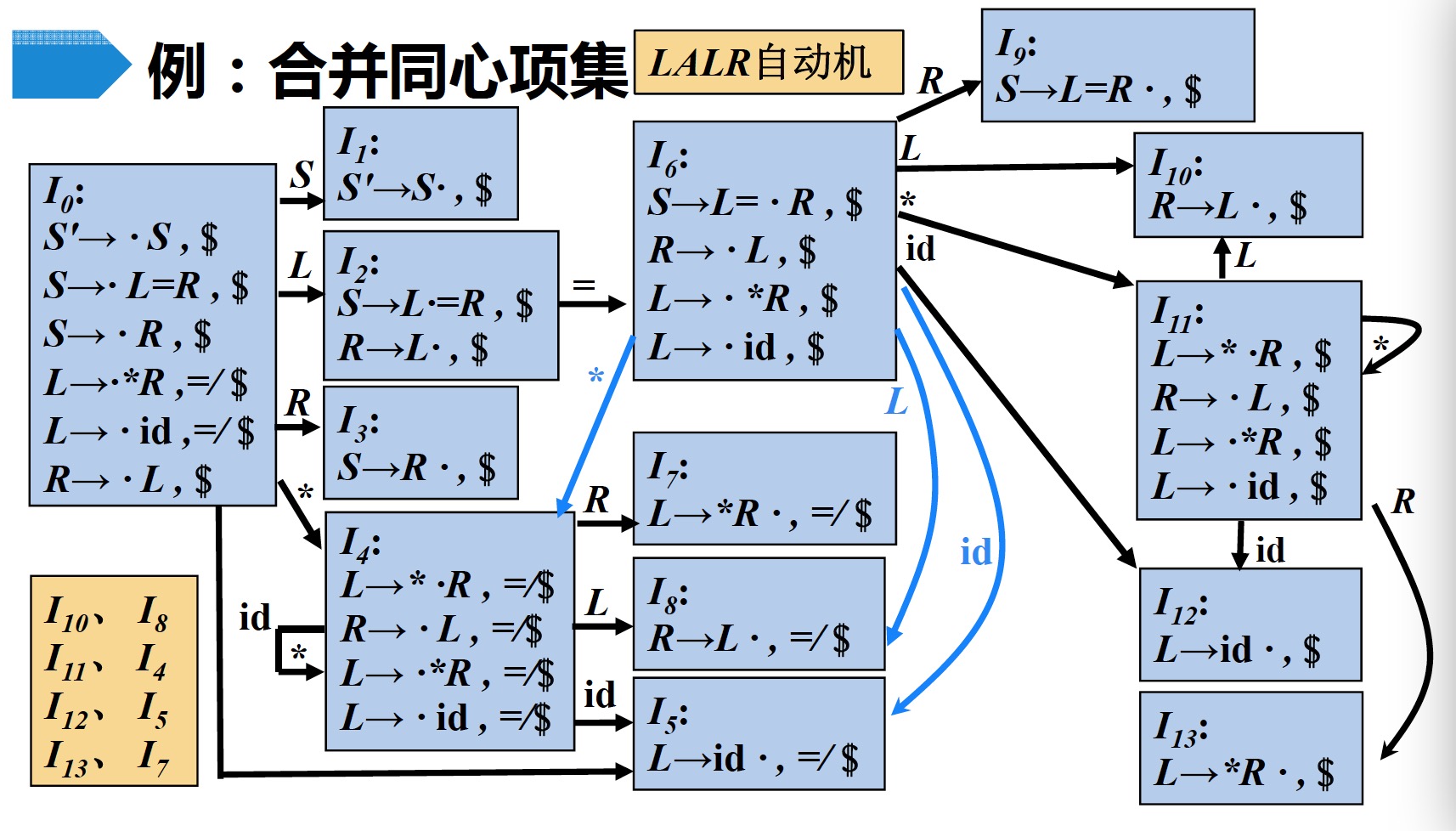
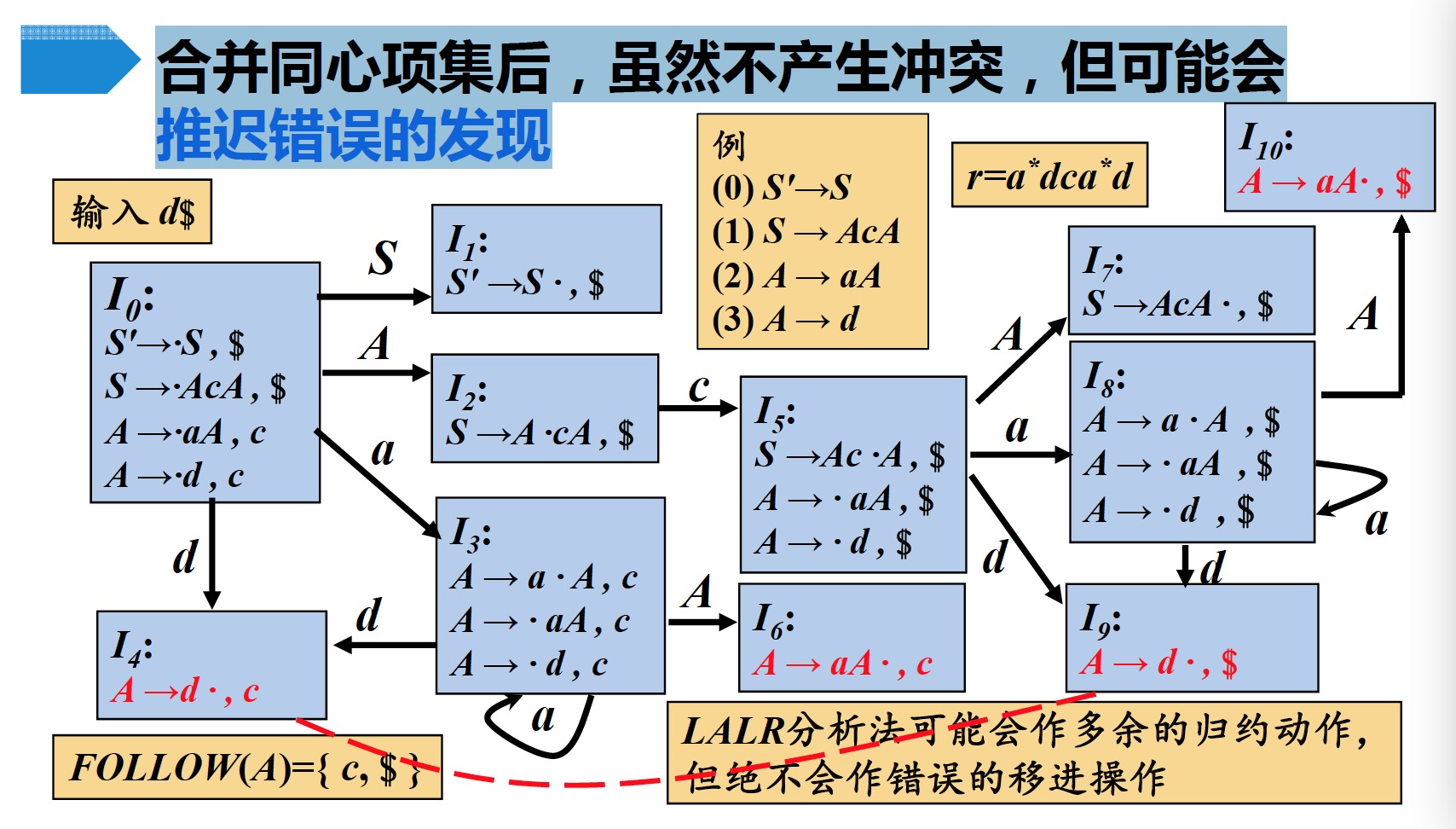
合并同心项集后,虽然不产生冲突,但可能会推迟错误的发现
3.3 $LALR(1)$的特点
- 形式上与$LR(1)$相同
- 大小上与$LR(0)/SLR$相当
- 分析能力介于$SLR$和$LR(1)$二者之间
4 二义性文法的$LR$分析
4.1 二义性文法的特点
- 每个二义性文法都不是$LR$的
- 某些类型的二义性文法在语言的描述和实现中很有用
4.2 例子
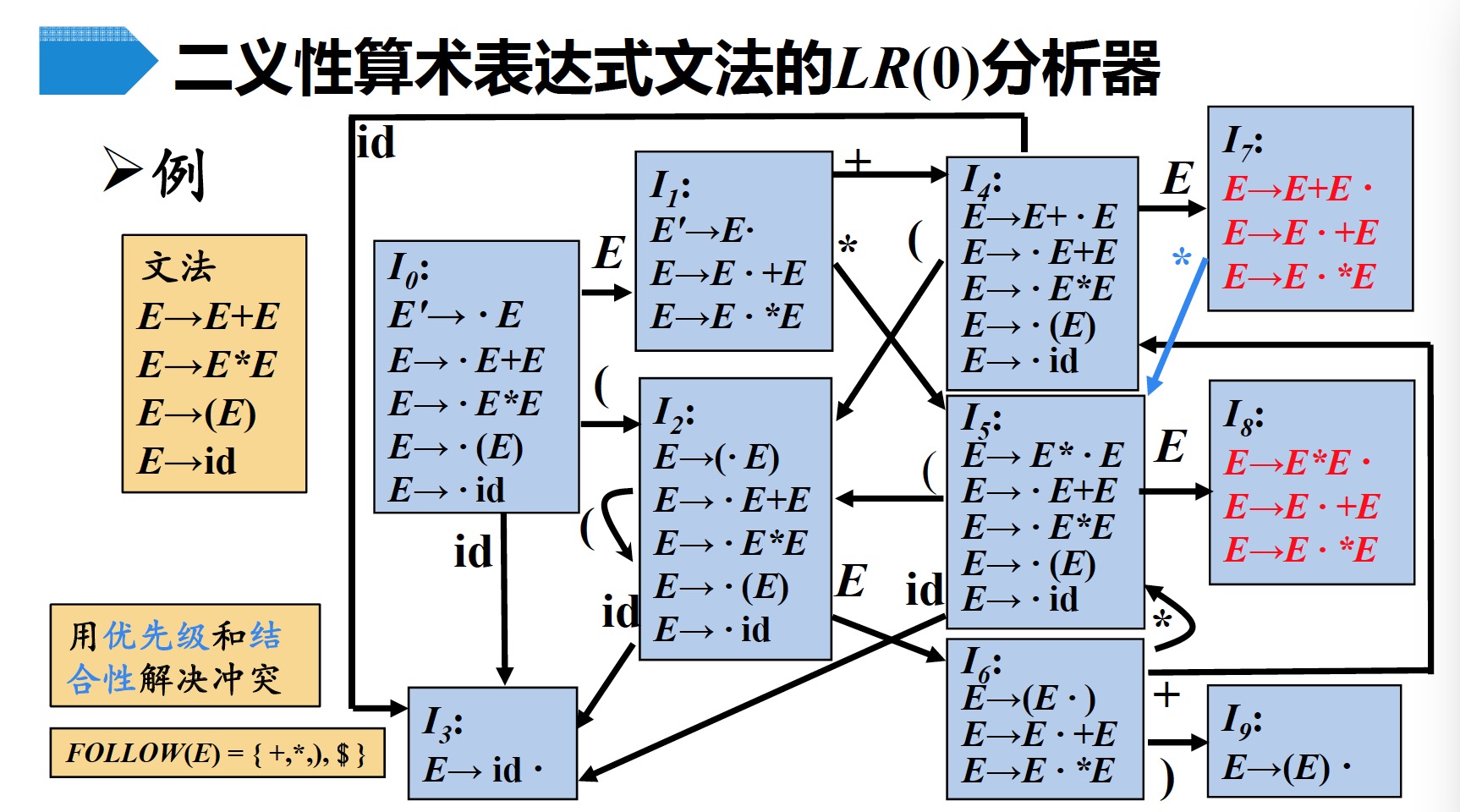
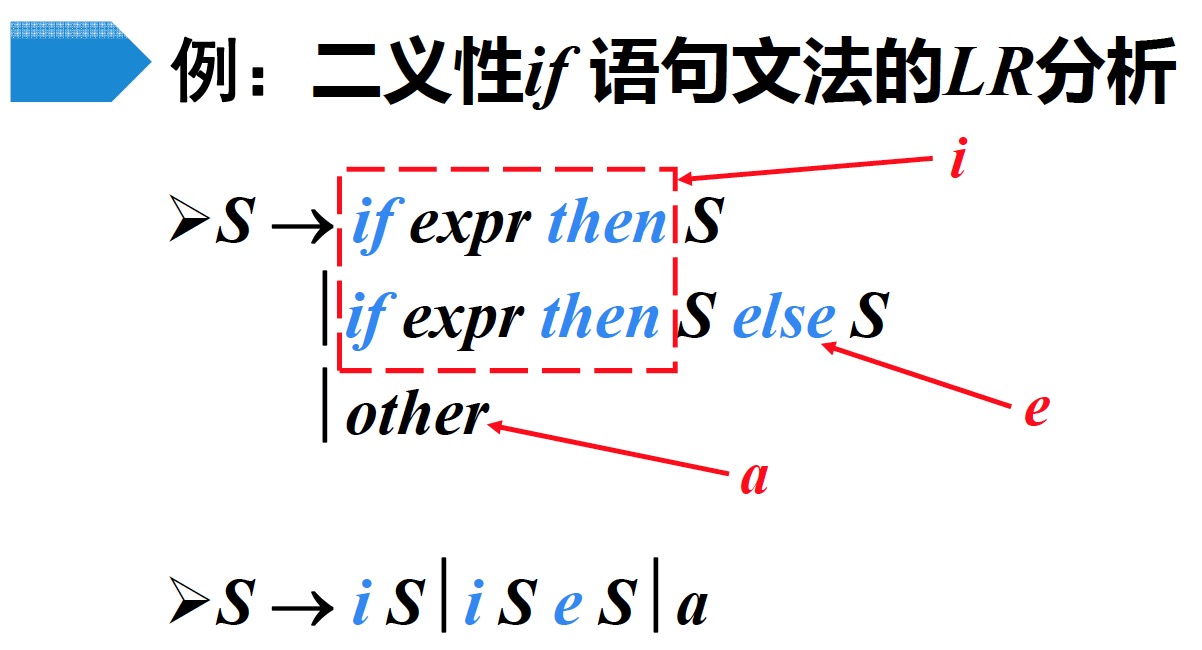
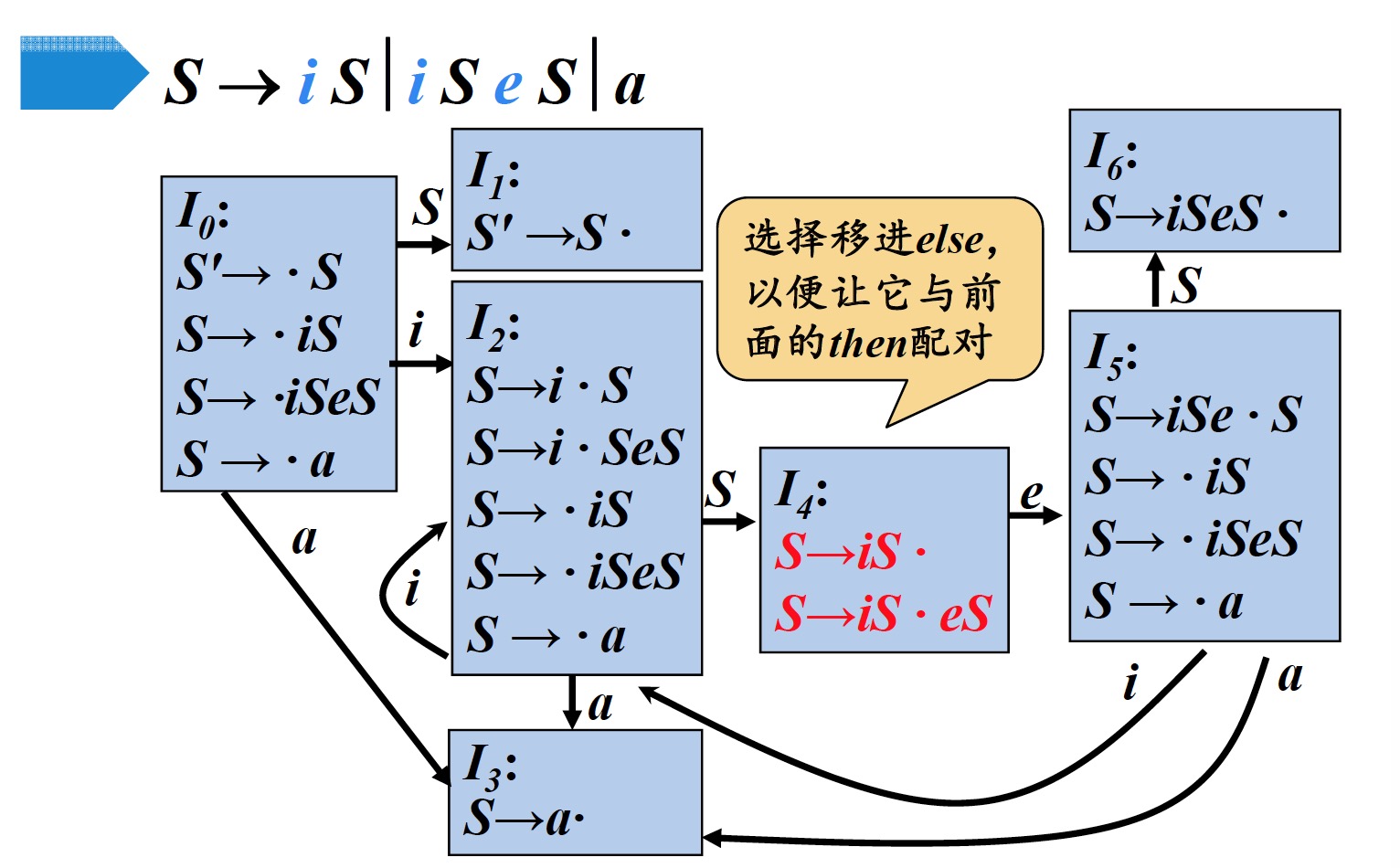
4.3 二义性文法的使用
应该保守地使用二义性文法,并且必须在严格控制之下使用,因为稍有不慎就会导致语法分析器所识别的语言出现偏差
5 LR分析中的错误处理
语法错误的检测
- 当$LR$分析器在查询分析表并发现一个报错条目时,就检测到了一个语法错误
错误恢复策略
- 恐慌模式错误恢复
- 短语层次错误恢复
5.1 恐慌模式错误恢复

- 从栈顶向下扫描,直到发现某个状态$s_i$,它有一个对应于某个非终结符$A$的$GOTO$目标(即后继状态),可以认为从这个$A$推导出的串中包含错误(哪里错了???)
- 然后丢弃0个或多个输入符号,直到发现一个可能合法地跟在$A$之后的符号$a$为止
- 之后将$s_{i+1} = GOTO(s_i , A)$压入栈中,继续进行正常的语法分析
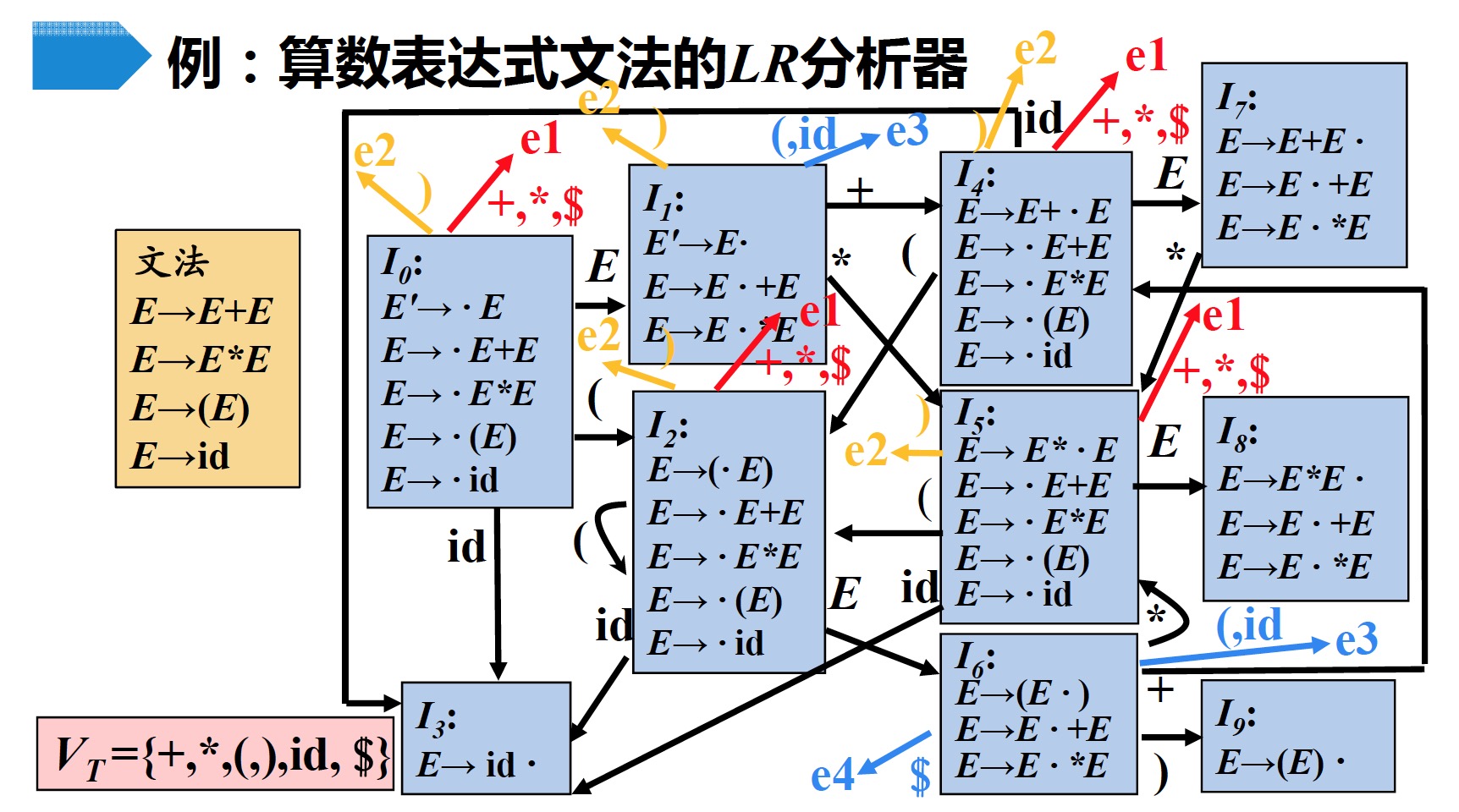
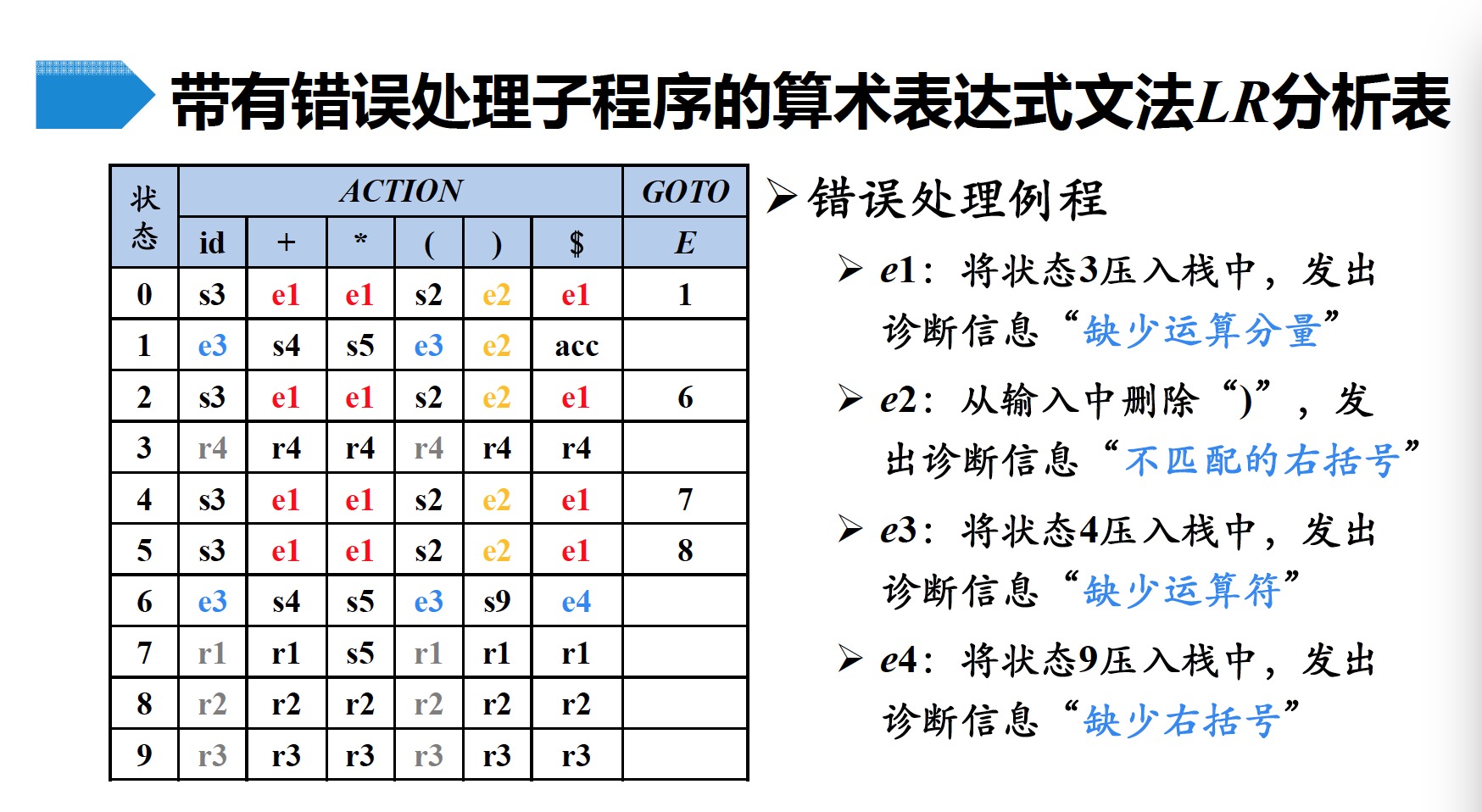
5.2 短语层次错误恢复
检查$LR$分析表中的每一个报错条目,并根据语言的使用方法来决定程序员所犯的何种错误最有可能引起这个语法错误。然后构造出适当的恢复过程
6 参考
- 《MOOC-编译原理-陈鄞》