阅读更多

1 自底向上分析概述

自底向上分析有如下特点

从分析树的底部(叶节点)向顶部(根节点)方向构造分析树
可以看成是将输入串$w$归约为文法开始符号$S$的过程
自顶向下的语法分析采用最左推导方式；自底向上的语法分析采用最左归约方式（反向构造最右推导）
自底向上语法分析的通用框架
- 移入-归约分析(Shift-Reduce Parsing)

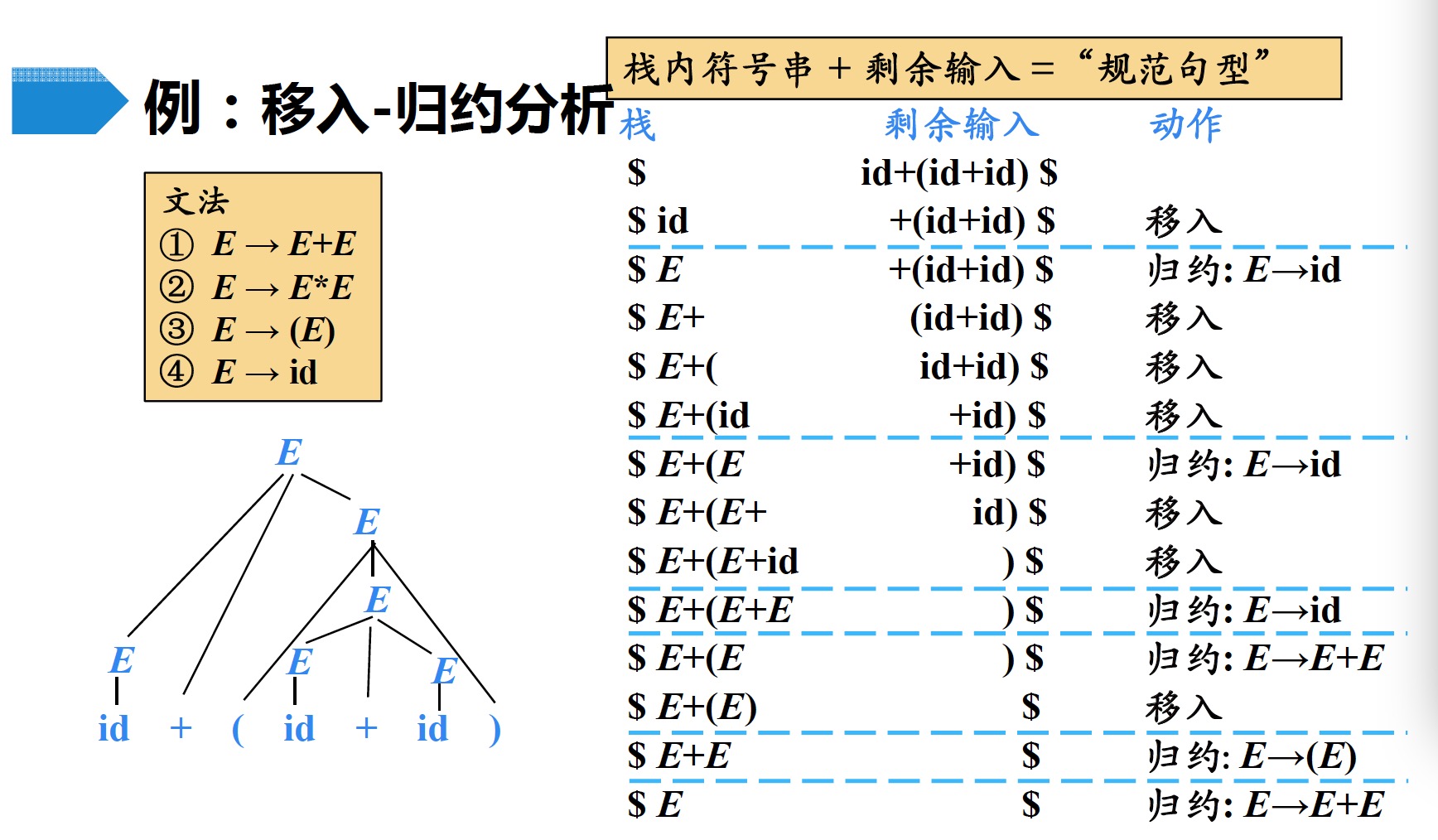
每次归约的符号串称为“句柄”

1.1 移入-归约分析的工作过程

在对输入串的一次从左到右扫描过程中，语法分析器将零个或多个输入符号移入到栈的顶端，直到它可以对栈顶的一个文法符号串$\beta$进行归约为止
然后，它将$\beta$归约为某个产生式的左部
语法分析器不断地重复这个循环，直到它检测到一个语法错误，或者栈中包含了开始符号且输入缓冲区为空(当进入这样的格局时，语法分析器停止运行，并宣称成功完成了语法分析)为止

1.2 移入-归约分析器可采取的4种动作

移入：将下一个输入符号移到栈的顶端
归约：被归约的符号串的右端必然处于栈顶。语法分析器在栈中确定这个串的左端，并决定用哪个非终结符来替换这个串
接收：宣布语法分析过程成功完成
报错：发现一个语法错误，并调用错误恢复子例程

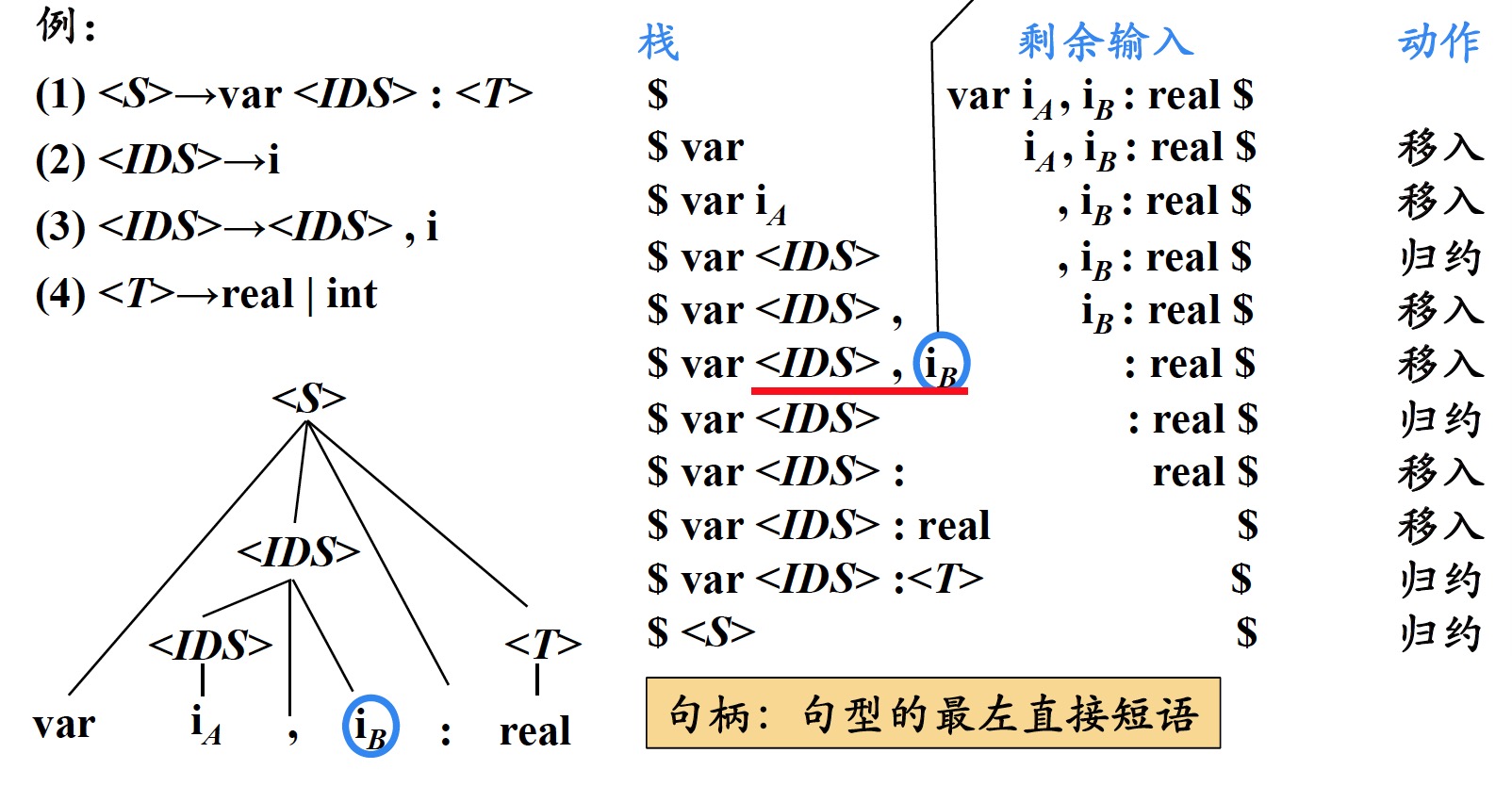
1.3 移入-归约分析中存在的问题

造成错误的原因：错误地识别了句柄

2 $LR$分析概述

2.1 $LR$分析法

首先，$LR$文法(Knuth, 1963) 是最大的、可以构造出相应移入-归约语法分析器的文法类

$L$: 对输入进行从左到右的扫描
$R$: 反向构造出一个最右推导序列

其次，$LR(k)$分析

需要向前查看$k$个输入符号的$LR$分析
$k = 0$和$k = 1$这两种情况具有实践意义。当省略$(k)$时，表示$k = 1$

2.2 $LR$分析法的基本原理

自底向上分析的关键问题是什么？

如何正确地识别句柄

句柄是逐步形成的，用“状态”表示句柄识别的进展程度

2.3 $LR$分析器（自动机）的总体结构

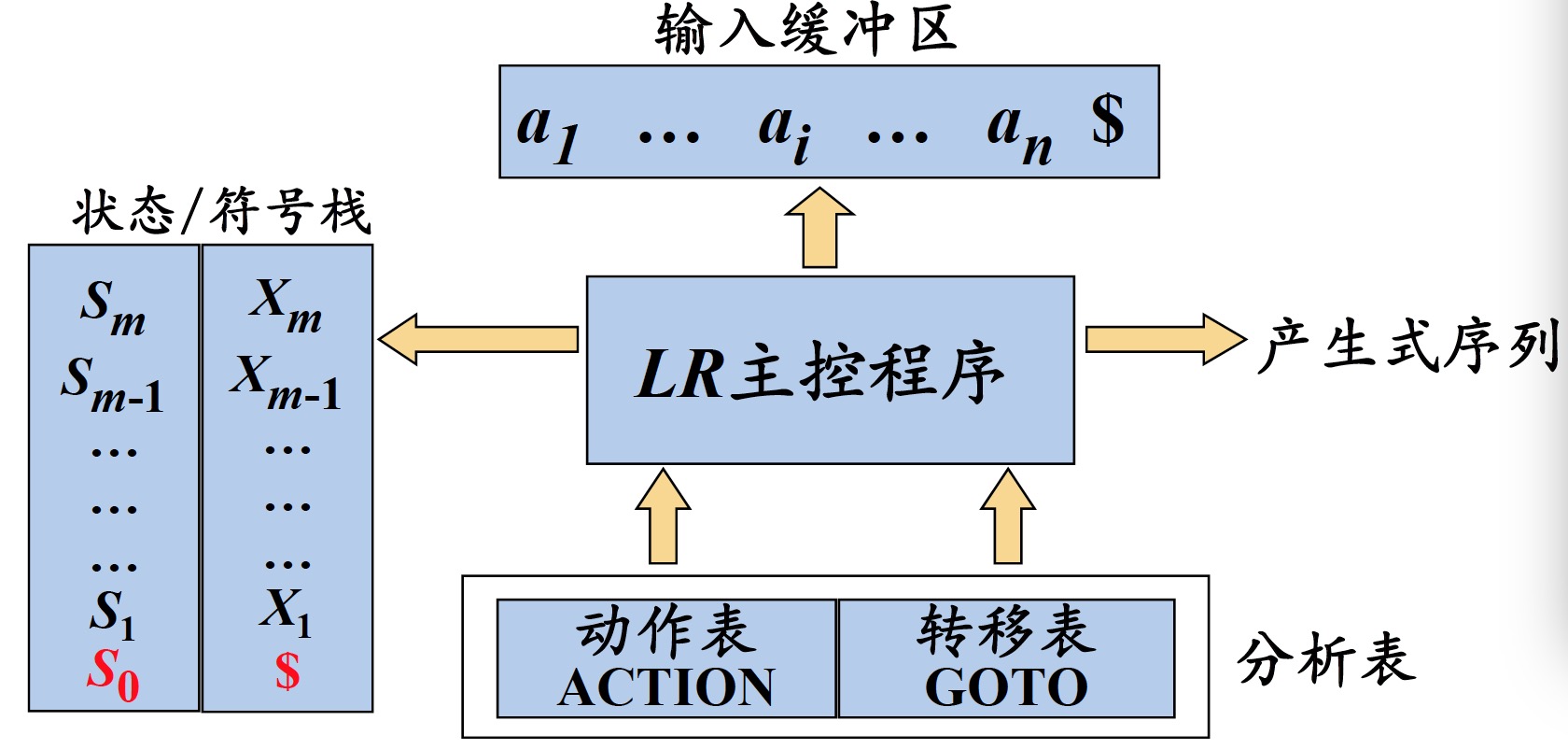
2.4 $LR$分析器的工作过程

初始化

$$\begin{split} 状态栈&：s_0 \\ 符号栈&：\$ \\ 剩余输入符号串&：a_1a_2...a_n \$ \\ \end{split}$$

一般情况

$$\begin{split} 状态栈&：s_0s_1...s_m \\ 符号栈&：\$X_1...X_m \\ 剩余输入符号串&：a_ia_{i+1}...a_n \$ \\ \end{split}$$

如果$ACTION[s_m, a_i]= sx$（移入动作），那么格局变为

$$\begin{split} 状态栈&：s_0s_1...s_m x \\ 符号栈&：\$X_1...X_m a_i \\ 剩余输入符号串&：a_{i+1}...a_n \$ \\ \end{split}$$

如果$ACTION[s_m, a_i]= rx$（归约动作），表示用第$x$个产生式$A→X_{m-(k-1)}...X_m$进行归约，那么格局变为

$$\begin{split} 状态栈&：s_0s_1...s_{m-k} \\ 符号栈&：\$X_1...X_{m-k}A \\ 剩余输入符号串&：a_ia_{i+1}...a_n \$ \\ \end{split}$$

- 若此时$GOTO[s_{m-k}, A] = y$，那么格局变为

$$\begin{split} 状态栈&：s_0s_1...s_{m-k}y \\ 符号栈&：\$X_1...X_{m-k}A \\ 剩余输入符号串&：a_ia_{i+1}...a_n \$ \\ \end{split}$$

如果$ACTION[s_m, a_i]=acc$，那么分析成功
如果$ACTION[s_m, a_i]=err$，那么出现语法错误

2.4.1 例子

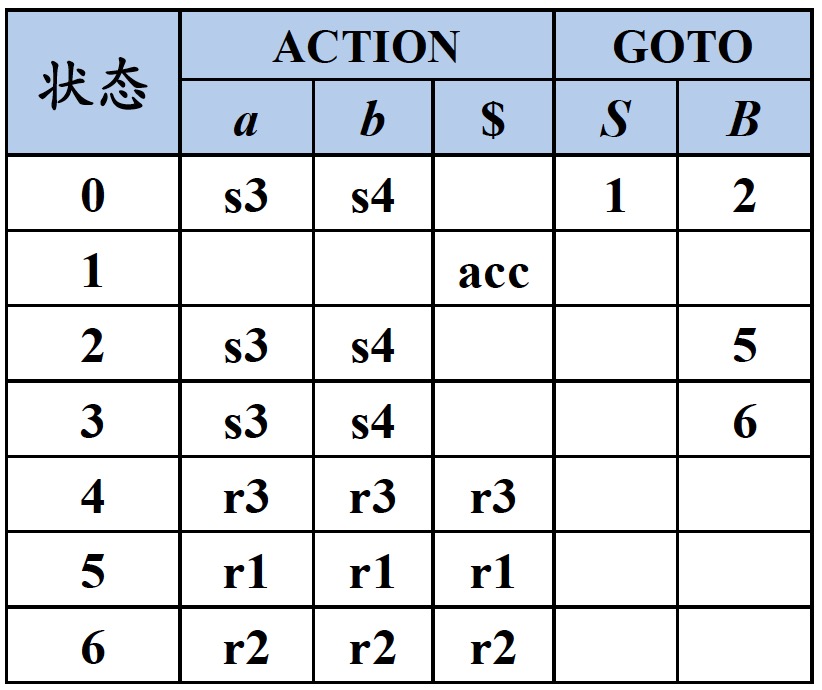
给定如下文法以及状态表

$$\begin{split} S^{\prime} &\to S \\ S &\to BB \\ B &\to aB \\ B &\to b \end{split}$$

分析过程如下

$$\begin{split} 状态栈&：0 \\ 符号栈&：\$ \\ 剩余输入符号&：bab\$ \\ &\Downarrow \\ 查表[0, b] &\to s4 \\ 状态栈&：04 \\ 符号栈&：\$b \\ 剩余输入符号&：ab\$ \\ &\Downarrow \\ 查表[4, a] &\to r3 \\ 状态栈&：0 \\ 符号栈&：\$B \\ 剩余输入符号&：ab\$ \\ &\Downarrow \\ 查表[0, B] &\to 2 \\ 状态栈&：02 \\ 符号栈&：\$B \\ 剩余输入符号&：ab\$ \\ &\Downarrow \\ 查表[2, a] &\to s3 \\ 状态栈&：023 \\ 符号栈&：\$Ba \\ 剩余输入符号&：b\$ \\ &\Downarrow \\ 查表[3, b] &\to s4 \\ 状态栈&：0234 \\ 符号栈&：\$Bab \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[4, \$] &\to r3 \\ 状态栈&：023 \\ 符号栈&：\$BaB \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[3, B] &\to 6 \\ 状态栈&：0236 \\ 符号栈&：\$BaB \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[6, \$] &\to r2 \\ 状态栈&：02 \\ 符号栈&：\$BB \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[2, B] &\to 5 \\ 状态栈&：025 \\ 符号栈&：\$BB \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[5, \$] &\to r1 \\ 状态栈&：0 \\ 符号栈&：\$S \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[0, S] &\to 1 \\ 状态栈&：01 \\ 符号栈&：\$S \\ 剩余输入符号&：\$ \\ &\Downarrow \\ 查表[1, \$] &\to acc \\ \end{split}$$

2.5 $LR$分析算法

输入：串$w$和$LR$语法分析表，该表描述了文法$G$的$ACTION$函数和$GOTO$函数
输出：如果$w$在$L(G)$中，则输出$w$的自底向上语法分析过程中的归约步骤；否则给出一个错误指示
方法：初始时，语法分析器栈中的内容为初始状态$s_0$，输入缓冲区中的内容为$w\$$。然后，语法分析器执行下面的程序：

2.6 如何构造给定文法的$LR$分析表

$LR(0)$分析
$SLR$分析
$LR(1)$分析
$LALR$分析

3 $LR(0)$分析

3.1 $LR(0)$项目

右部某位置标有圆点的产生式称为相应文法的一个$LR(0)$项目（简称为项目）

$$A \to \alpha_1 \cdot \alpha_2 $$

3.2 增广文法(Augmented Grammar)

如果$G$是一个以$S$为开始符号的文法，则$G$的增广文法$G^{\prime}$ 就是在$G$中加上新开始符号$S^{\prime}$和产生式$S^{\prime} \to S$而得到的文法

引入这个新的开始产生式的目的是使得文法开始符号仅出现在一个产生式的左边，从而使得分析器只有一个接受状态

3.2.1 后继项目

同属于一个产生式的项目，但圆点的位置只相差一个符号，则称后者是前者的后继项目

$A \to \alpha \cdot X \beta$的后继项目是$A \to \alpha X \cdot \beta$

3.2.2 项目集闭包

可以把等价的项目组成一个项目集(I) ，称为项目集闭包(Closure of Item Sets)，每个项目集闭包对应着自动机的一个状态

例如，给定文法$G$

$$\begin{split} S^{\prime} &\to S \\ S &\to BB \\ B &\to aB \\ B &\to b \end{split}$$

其中一个闭包如下

$$\begin{split} I_0: \\ S^{\prime} &\to \cdot S \\ S &\to \cdot BB \\ B &\to \cdot aB \\ B &\to \cdot b \end{split}$$

3.2.3 例：$LR(0)$自动机

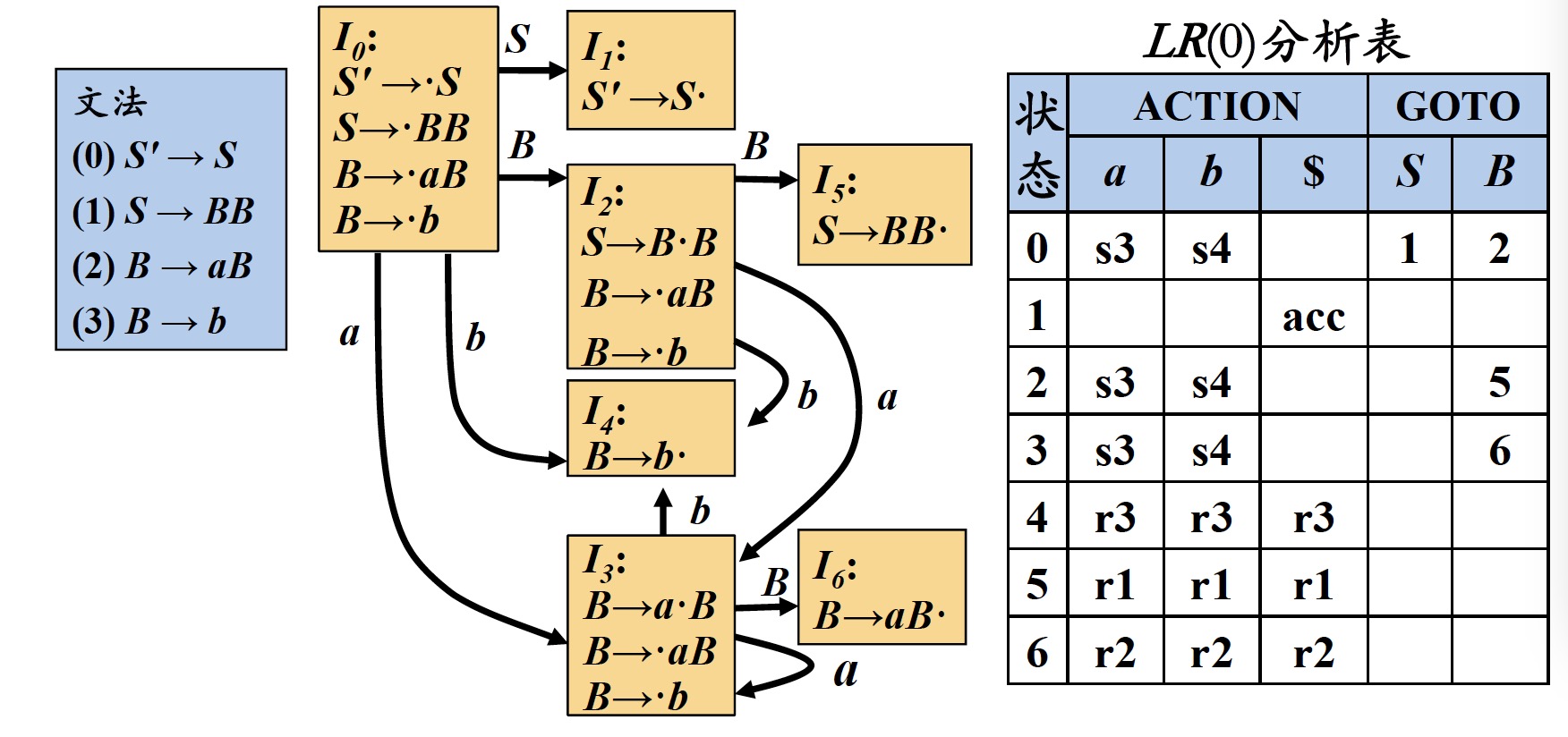
4 $LR(0)$分析表构造算法

4.1 $CLOSURE()$函数

计算给定项目集$I$的闭包

$$CLOSURE(I) = I \cup \{ B \to \cdot \gamma | A \to \alpha \cdot B \beta \in CLOSURE(I), B \to \gamma \in P \}$$

4.2 $GOTO()$函数

返回项目集$I$对应于文法符号$X$的后继项目集闭包

$$GOTO(I, X) = CLOSURE(\{ A \to \alpha X \cdot \beta | A \to \alpha \cdot X \beta \in I \})$$

4.3 构造$LR(0)$自动机的状态集

规范$LR(0)$项集族(Canonical $LR(0)$ Collection)

$$C = \{ I_0 \} \cup \{ I | \exists J \in C, X \in V_N \cup V_T, I = GOTO(J, X) \}$$

4.4 $LR(0)$分析表构造算法

构造$G^{\prime}$的规范$LR(0)$项集族$C = \{ I_0, I_1,... , I_n \}$
令$I_i$对应状态$i$。状态$i$的语法分析动作按照下面的方法决定：
- $\textbf{if}\; A \to \alpha \cdot a \beta \in I_i \;\textbf{and}\; GOTO(I_i, a) = I_j \;\textbf{then}\; ACTION[i, a] = sj$
- $\textbf{if}\; A \to \alpha \cdot B \beta \in I_i \;\textbf{and}\; GOTO(I_i, B) = I_j \;\textbf{then}\; GOTO[i, B] = j$
- $\textbf{if}\; A \to \alpha \cdot \in I_i 且 A \ne S^{\prime} \;\textbf{then}\; \;\textbf{for}\; \forall a \in V_T \cup \{ \$ \} \;\textbf{do}\; ACTION[i, a] = rj$（$j$是产生式$A \to \alpha$的编号）
- $\textbf{if}\; S^{\prime} \to S \cdot \in I_i \;\textbf{then}\; ACTION [ i,\$] = acc$
没有定义的所有条目都设置为“error”

4.5 $LR(0)$自动机的形式化定义

文法

$$G = ( V_N, V_T, P, S )$$

$LR(0)$自动机

$$M = ( C, V_N \cup V_T, GOTO, I_0, F )$$

$C = \{I_0 \} \cup \{ I | \exists J \in C, X \in V_N \cup V_T, I = GOTO(J,X) \}$
$I_0 = CLOSURE(\{ S^{\prime} \to \cdot S \})$
$F = \{ CLOSURE(\{ S^{\prime} \to S \cdot \}) \}$

4.6 移进/归约冲突和归约/归约冲突

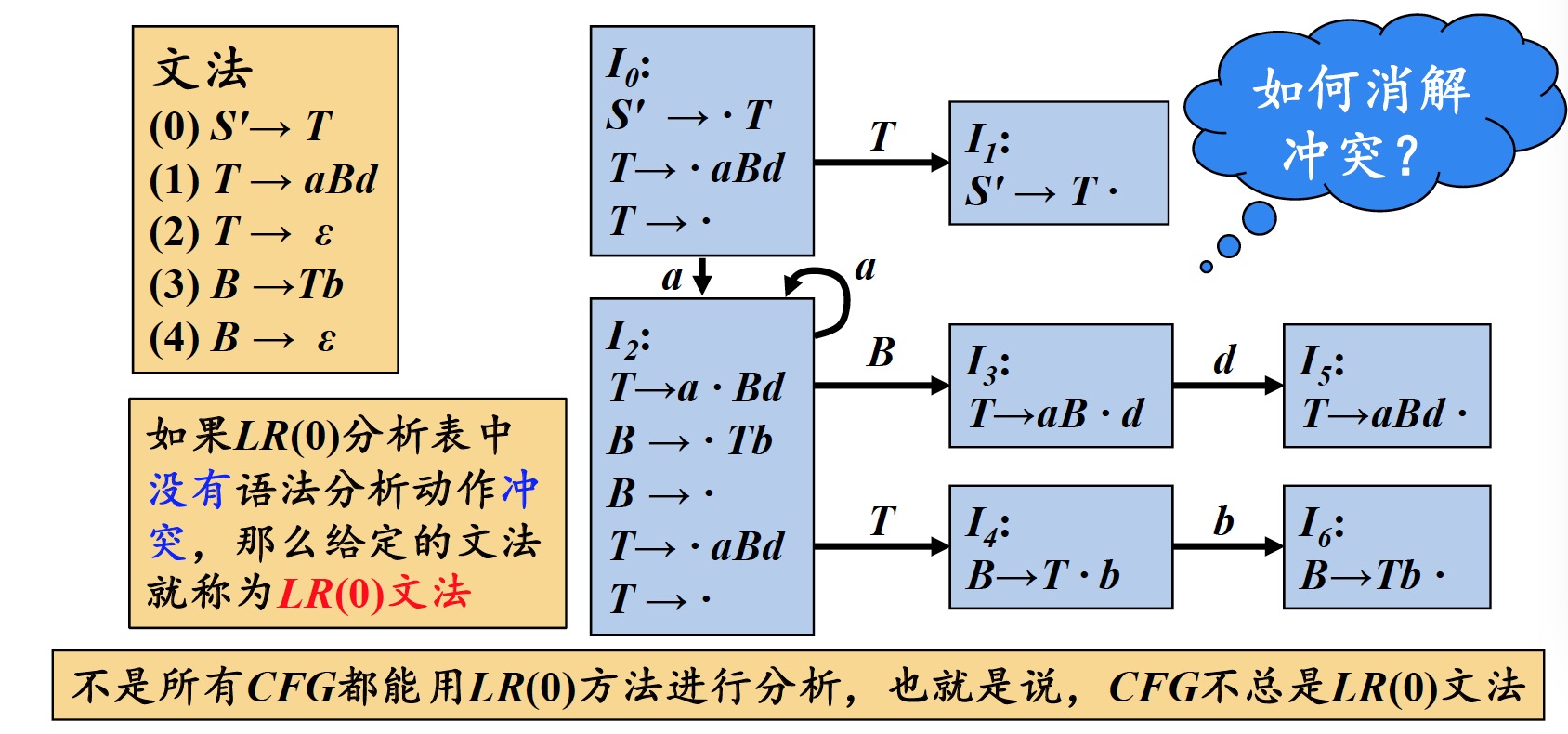
在项目集闭包$I_2$中

$B \to \cdot$与$T \to \cdot$会产生归约/归约冲突，即不知道使用哪个进行归约
$B \to \cdot$与$T \to a \cdot Bd$会产生移进/归约冲突，即不知道该移进还是该归约

5 参考

《MOOC-编译原理-陈鄞》

Liuye Notebook

编译原理-语法分析3