阅读更多
1 基本概念
1.1 字母表
字母表$\sum$是一个有穷符号集合
- 符号:字母、数字、标点符号、…
例:
- 二进制字母表:{ 0,1 }
- ASCII字符集
- Unicode字符集
1.1.1 字母表上的运算
字母表$\sum_1$和$\sum_2$的乘积(product)
- $\sum_1 \sum_2 = \{ ab | a \in \sum_1, b \in \sum_2 \}$
字母表$\sum$的n次幂(power)
- $\begin{cases} \sum^0 = \{ \varepsilon \}\\ \sum^n = \sum^{n-1} \sum, n \ge 1 \end{cases}$
字母表$\sum$的正闭包(positive closure),即长度为正数的符号串构成的集合
- $\sum^+ = \sum \cup \sum^2 \cup \sum^3 ...$
字母表$\sum$的克林闭包(Kleene closure),任意符号串构成的集合
- $ \sum^* = \sum^0 \cup \sum^+ = \sum^0 \cup \sum \cup \sum^2 \cup \sum^3 ...$
1.2 串
设$\sum$是一个字母表,$\forall x \in \sum^*$,$x$称为是$\sum$上的一个串
- 串是字母表中符号的一个有穷序列
- 串s的长度,通常记作$|s|$,是指s中符号的个数
- 空串是长度为0的串,用$\varepsilon$(epsilon)表示
1.2.1 串上的运算
如果$x$和$y$是串,那么$x$和$y$的连接(concatenation)是把$y$附加到$x$后面而形成的串,记作$xy$
- 空串是连接运算的单位元(identity),即对于任何串$s$都有,$\varepsilon s = s \varepsilon = s$
串$s$的幂运算
- $\begin{cases} s^0 = \{ \varepsilon \}\\ s^n = s^{n-1} s, n \ge 1 \end{cases}$
2 文法的定义
2.1 文法的形式化定义
文法可以用数学符号$G = (V_T, V_N, P, S)$表示
- $V_T$:终结符集合。终结符(terminal symbol)是文法所定义的语言基本符号,有时也称为token。换言之,就是原子的,不可再分的(例如英文中的单词就是终结符)
- $V_N$:非终结符集合。非终结符(nonterminal)是用来表示语法成分的符号,有时也称为语法变量。换言之,就是非原子的,可再分的(例如
<句子>,<名词短语>,<动词短语>) - $P$:产生式集合。产生式(production)描述了将终结符和非终结符组合成串的方法。产生式的一般形式为:$$\alpha \to \beta$$
- $\alpha \in (V_T \cup V_N)^+$,且$\alpha$中至少包含$V_N$中的一个元素,称为产生式的头(head)或左部(left side)
- $\beta \in (V_T \cup V_N)^*$,称为产生式的体(body)或右部(right side)
- $S$:开始符号。$S \in V_N$。开始符号(start symbol)表示的是该文法中最大的语法成分
- 另外,$V_T$与$V_N$满足
- $V_T \cap V_N = \Phi$
- $V_T \cup V_N = 文法符号集$
- 终结符(terminal symbol)与非终结符(nonterminal)统称为文法符号
2.2 产生式的简写
对一组有相同左部的$\alpha$产生式
$$\alpha \to \beta_1, \alpha \to \beta_2, ..., \alpha \to \beta_n$$可以简记为
$$\alpha \to \beta_1 | \beta_2 | ... | \beta_n$$其中,$\beta_1, \beta_2, ..., \beta_n$称为$\alpha$的候选式
2.3 符号约定
下述符号是终结符
- 字母表中排在前面的小写字母,如a、b、c
- 运算符,如+、*等
- 标点符号,如逗号、括号等
- 数字,0,1,2,…,9
- 粗体字符串,如id,if等
下述符号是非终结符
- 字母表中排在前面的大写字母
- 字母S,通常表示开始符号
- 小写、斜体的名字,如expr、stmt等
- 代表程序构造的大写字母
- E:表达式
- T:项
- F:因子
其他规则
- 字母表中排在后面的大写字母,如X、Y、Z,表示文法符号(即终结符或非终结符)
- 字母表中排在后面的小写字母,主要是u、v、…、z,表示终结符号串(包括空串)
- 小写希腊字母,如$\alpha, \beta, \gamma$,表示文法符号串(包括空串)
- 除非特别说明,第一个产生式的左部就是开始符号
3 语言的定义
3.1 推导和归约
给定文法$G = (V_T, V_N, P, S)$,如果$\alpha \to \beta \in P$,那么可以将符号串$\gamma \alpha \delta$中的$\alpha$替换为$\beta$,也就是说,将$\gamma \alpha \delta$重写(rewrite)为$\gamma \beta \delta$,记作$\gamma \alpha \delta \Rightarrow \gamma \beta \delta$。此时称文法中的符号串$\gamma \alpha \delta$直接推导出$\gamma \beta \delta$
- 简而言之,就是用产生式的右部替换产生式的左部
如果$\alpha_0 \Rightarrow \alpha_1, \alpha_1 \Rightarrow \alpha_2, ..., \alpha_{n-1} \Rightarrow \alpha_n$,则可以记作$\alpha_0 \Rightarrow \alpha_1 \Rightarrow \alpha_2 \Rightarrow ... \Rightarrow \alpha_{n-1} \Rightarrow \alpha_n$。称符号串$\alpha_0$经过n步推导出$\alpha_n$,简记为$\alpha_0 \Rightarrow^n \alpha_n$
- $\alpha \Rightarrow^0 \alpha$
- $\Rightarrow^+$表示“经过正数步推导”
- $\Rightarrow^*$表示“经过若干(可以是0)步推导”
归约就是推导的逆过程
如何判断某一词串是否是该语言的句子
- 句子的推导–从生成语言的角度
- 句子的归约–从识别语言的角度
3.2 句型和句子
如果$S \Rightarrow^* \alpha, \alpha \in (V_T \cup V_N)^*$,则称$\alpha$是$G$的一个句型(sentential form)
- 一个句型中既可以包含终结符,又可以包含非终结符,也可能是空串
如果$S \Rightarrow^* w, w \in V_T^*$,则称$w$是$G$的一个句子
- 句子是不包含非终结符的句型
3.3 语言的形式化定义
由文法$G$的开始符号$S$推导出的所有句子构成的集合称为文法$G$生成的语言,记为$L(G)$,即$$L(G) = \{ w | S \Rightarrow^* w, w \in V_T^*\}$$
4 Chomsky文法分类体系
4.1 0型文法(Type-0 Grammar)
$$\alpha \to \beta$$0型文法又称为无限制文法(Unrestricted Grammar)或短语结构文法(Phrase Structure Grammar, PSG)
- $\forall \alpha \to \beta \in P$,$\alpha$中至少包含1个非终结符
0型语言:由0型文法$G$生成的语言$L(g)$
4.2 1型文法(Type-1 Grammar)
$$\alpha \to \beta$$1型文法又称为上下文有关的文法(Context-Sensitive Grammar, CSG)
- $\forall \alpha \to \beta \in P, |\alpha| \le |\beta|$
- 产生式的一般形式:$\alpha_1 A \alpha_2 \to \alpha_1 \beta \alpha_2, \beta \ne \varepsilon$
1型语言(上下文有关语言):由上下文有关文法(1型文法)$G$生成的语言$L(g)$
4.3 2型文法(Type-2 Grammar)
$$\alpha \to \beta$$2型文法又称为上下文无关文法(Context-Free Grammar, CFG)
- $\forall \alpha \to \beta \in P, \alpha \in V_N$
- 产生式的一般形式:$A \to \beta$
2型语言(上下文无关语言):由上下文无关文法(2型文法)$G$生成的语言$L(g)$
4.4 3型文法(Type-3 Grammar)
$$\alpha \to \beta$$3型文法又称为正则文法(Regular Grammar, RG)
- 右线性(Right Linear)文法:$A \to wB$或$A \to w$
- 左线性(Left Linear)文法:$A \to Bw$或$A \to w$
3型语言(正则语言):由正则文法(3型文法)$G$生成的语言$L(g)$
4.5 四种文法之间的关系
逐级限制
- 0型文法:$\alpha$中至少包含一个终结符
- 1型文法(CSG):$|\alpha| \le |\beta|$
- 2型文法(CFG):$\alpha \in V_N$
- 3型文法(RG):$A \to wB$或$A \to w$($A \to Bw$或$A \to w$)
逐级包含
- 0型文法包含1型文法
- 1型文法包含2型文法
- 2型文法包含3型文法
5 文法的分类
5.1 CFG分析树
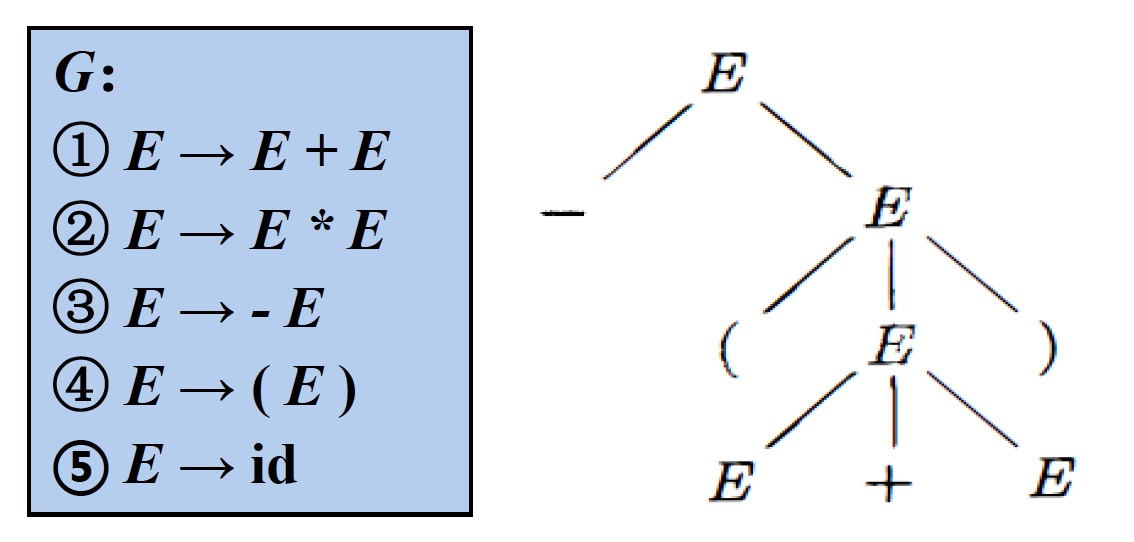
- 根节点的标号为文法开始符号
- 内部节点表示对一个产生式$A \to \beta$的应用,该节点的标号是此产生式左部$A$。该节点的子节点标号从左到右构成了产生式的右部$\beta$
- 叶节点的标号既可以是非终结符,也可以是终结符。从左到右排列叶节点得到的符号串称为是这棵树的产出(yield)或边缘(frontier)
给定一个推导$S \Rightarrow \alpha_1 \Rightarrow \alpha_2 \Rightarrow ... \Rightarrow \alpha_n$,对于推导过程中的每一个句型$a_i$,都可以构造出一个边缘为$a_i$的分析树
5.2 短语
给定一个句型,其分析树中每一棵子树的边缘,称为该句型的一个短语(phrase)
- 如果子树只有父子两代节点,那么这棵子树的边缘称为该句型的一个直接短语
- 直接短语一定是某产生式的右部
- 产生式的右部不一定是给定句型的直接短语,即这个产生式的右部不构成一对父子节点
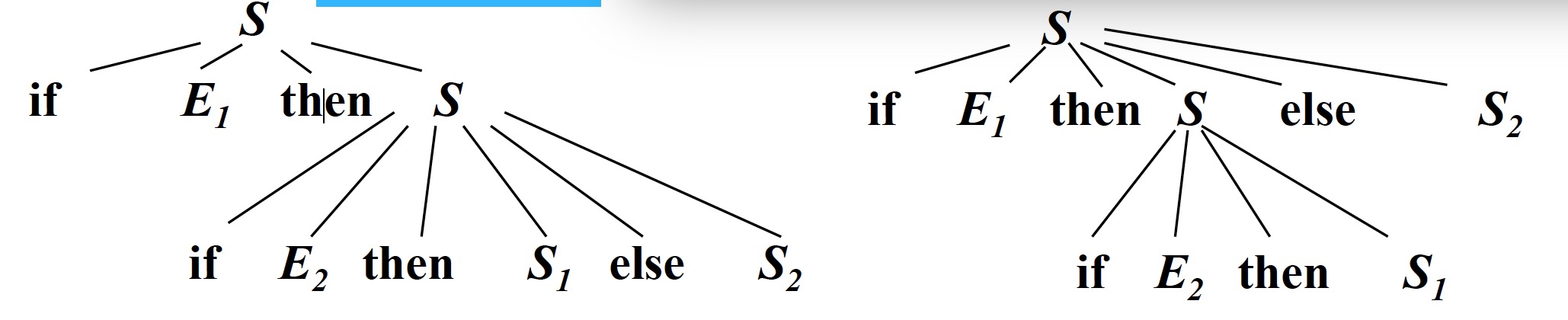
5.3 二义性文法
如果一个文法可以为某个句子生成多棵分析树,则称这个文法是二义性的
例如
给定文法$G$,满足$$S \to \textbf{if}\;\;E\;\;\textbf{then}\;\;S\;\;|\;\;\textbf{if}\;\;E\;\;\textbf{then}\;\;S\;\;\textbf{else}\;\;S\;\;|\;\;other$$
给定句型:$$\textbf{if}\;\;E_1\;\;\textbf{then}\;\;\textbf{if}\;\;E_2\;\;\textbf{then}\;\;S_1\;\;\textbf{else}\;\;S_2$$
消除歧义:每个else和最近的尚未匹配的if匹配
二义性文法的判定:对于任意一个上下文无关文法,不存在一个算法,判定它是无二义性的。但能给出一个充分条件,满足这组充分条件的文法一定是无二义性的
- 满足,肯定无二义性
- 不满足,未必有二义性
6 参考
- 《MOOC-编译原理-陈鄞》
- Latex所有常用数学符号整理