Algorithm-SSSP

阅读更多

1 Dijkstra

Dijkstra 算法（中文名：迪杰斯特拉算法）是由荷兰计算机科学家 Edsger Wybe Dijkstra 提出。该算法常用于路由算法或者作为其他图算法的一个子模块。举例来说，如果图中的顶点表示城市，而边上的权重表示城市间开车行经的距离，该算法可以用来找到两个城市之间的最短路径

注意该算法要求图中不存在负权边。

1.1 算法描述

设G=(V,E)是一个带权有向图，把图中顶点集合V分成两组，第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径，就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了）；第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。在加入的过程中，总保持从源点v到S中各顶点的最短路径长度不大于从源点v到U中任何顶点的最短路径长度

此外，每个顶点i对应一个距离D(i)

• S中的顶点的距离就是从v到此顶点的最短路径长度
• U中的顶点的距离，是从v到此顶点只包括S中的顶点为中间顶点的当前最短路径长度。即迭代过程中的当前时刻的最短路径，之后可能会被更新

1.2 流程

为了方便理解，给出以下流程图

flowchart TD
    st(["开始"])
    op1["将源节点v加入S集合
并初始化D"]
    op2["从集合U中找到D(i∈U)
最小的顶点i，将其从集
合U中删除，并添加到集
合S中"]
    op3["更新集合U中顶点j的距离
D(j)=min(D(j),D(i)+path(i,j))"]
    cond1{"集合U为空 ?"}
    en(["结束"])

    st --> op1
    op1 --> op2
    op2 --> op3
    op3 --> cond1
    cond1 --> |yes| en
    cond1 --> |no| op2

1.3 Java源码

对应HihoCode第1081题。可自行验证正确性

package org.liuyehcf.graph;

import java.util.Arrays;
import java.util.Scanner;

/**
 * Created by t-chehe on 8/5/2017.
 */
public class Dijkstra {
    private static final int CANNOT_REACH = Integer.MAX_VALUE >> 2;

    public static void main(String[] args) {
        //edgeNum并不代表真正有效边的数量，因为相同的源节点和目的节点之间可能有多条道路，我们只需要保留最小的即可
        int vertexNum, edgeNum, source, dest;

        Scanner scanner = new Scanner(System.in);

        vertexNum = scanner.nextInt();
        edgeNum = scanner.nextInt();
        source = scanner.nextInt();
        dest = scanner.nextInt();

        int[][] graph = new int[vertexNum + 1][vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            Arrays.fill(graph[i], CANNOT_REACH);
            graph[i][i] = 0;
        }

        while (--edgeNum >= 0) {
            int s = scanner.nextInt();
            int d = scanner.nextInt();
            int l = scanner.nextInt();

            //题意中的道路是双向都可通的，因此对于有向图来说两个方向都需要存
            if (l < graph[s][d]) {
                graph[s][d] = l;
                graph[d][s] = l;
            }
        }

        System.out.println(minPath(graph, vertexNum, source, dest));
    }

    public static int minPath(int[][] graph, int vertexNum, int source, int dest) {
        //visited将节点集合分为两部分，true代表已访问（记为集合S），false代表未访问(记为集合U)
        boolean[] visited = new boolean[vertexNum + 1];

        int[] distance = new int[vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            distance[i] = graph[source][i];
        }

        distance[source] = 0;

        for (int i = 2; i <= vertexNum; i++) {
            int minLength = CANNOT_REACH;
            int nextVertex = -1;

            //在所有未访问的节点中找到距离source最近的节点
            for (int j = 1; j <= vertexNum; j++) {
                if (!visited[j]
                        && distance[j] < minLength) {
                    nextVertex = j;
                    minLength = distance[j];
                }
            }

            visited[nextVertex] = true;

            //如果source与j(j在集合U中)可以通过节点nextNode相连，那么更新source与j的距离
            for (int j = 1; j <= vertexNum; j++) {
                if (!visited[j]
                        && distance[nextVertex] + graph[nextVertex][j] < distance[j]) {
                    distance[j] = distance[nextVertex] + graph[nextVertex][j];
                }
            }
        }

        return distance[dest];
    }
}

2 Floyd-Warshall

Floyd-Warshall算法（Floyd-Warshall algorithm）是解决任意两点间的最短路径的一种算法，可以正确处理有向图或负权的最短路径问题，同时也被用于计算有向图的传递闭包。Floyd-Warshall算法的时间复杂度为O(N3)，空间复杂度为O(N2)

2.1 算法描述

Floyd-Warshall算法本质上来说就是动态规划，我们首先从子问题的设计入手。令F[k][i][j]代表仅包含前k个节点作为中间节点的情况下，节点i到节点j的最短距离

于是我们可以给出递推表达式：F[k][i][j] = min(F[k-1][i][j], F[k-1][i][k] + F[k-1][k][j])。其中F[k-1][i][j]代表当不选取第k个节点作为中间节点时的最短距离；F[k-1][i][k] + F[k-1][k][j]代表选取第k个节点作为中间节点时的最短距离

2.1.1 空间降维

可以看出F[k][i][j]仅仅与F[k-1][?][?]有关，于是空间复杂度可以从O(N3)降低为O(N2)，此时递推表达式变为F[i][j] = min(F[i][j], F[i][k] + F[k][j])

注意，最好对i和j降序遍历，否则可能得到错误的结果(对于Floyd算法，升序遍历可能得到正确的结果，但是对于其他DP问题，例如0-1背包问题就可能得到错误的结果)。因为F[i][j]依赖于F[i][k]和F[k][j]，因此必须保证在计算过程k的F[i][j]时，使用的是过程k-1的F[i][k]和F[k][j]。如果升序遍历，那么得到的F[i][j]可能经过了两次顶点k，因为F[i][k]和F[k][j]已经是过程k的最优解，因此可能经过顶点k，幸运的是，F[k][k] = 0，即F[i][k]和F[k][j]在过程k-1和过程k中的值必然是一样的，因此不会对结果造成影响

2.1.2 0-1背包的空间降维

类似地，0-1背包问题的空间复杂度也可以进行降维处理。0-1背包的子问题设计如下，令M[k][i]代表前k个物品在给定容量i时的最大收益。P[i]代表第i个物品的收益，V[i]代表第i个物品的容量

于是我们可以给出递推表达式：M[k][i] = min(M[k-1][i], V[i] + M[k-1][i - V[i]])。其中M[k-1][i]代表当不选取第k个物品时的最大收益；V[i] + M[k-1][i - V[i]]代表不选取第k个物品时的最大收益

可以看出M[k][i]仅仅与M[k-1][?]有关，于是空间复杂度可以从O(MN)降低为O(N)。此时递推表达式变为M[i] = min(M[i], V[i] + M[i - V[i]])

注意，必须对容量i降序遍历，否则将得到错误结。因为M[i]依赖于M[i - V[i]]，因此必须保证在计算过程k的M[i]时，使用的是过程k-1的M[i - V[i]]。如果升序遍历，那么得到的M[i]可能包含两个物品k的受益，因为M[i - V[i]]已经是过程k的最优值，因此可能就包含了物品k

package org.liuyehcf.dp.backpack;

import java.util.Random;

/**
 * Created by liuye on 2017/4/10 0010.
 */
public class TestBaseBackPack {
    public static void main(String[] args) {
        Random random = new Random(0);
        for (int time = 0; time < 100; time++) {

            int N = random.nextInt(100) + 1, V = random.nextInt(1000) + 1;
            int W = random.nextInt(50) + 1, C = random.nextInt(50) + 1;
            int[] weights = new int[N];
            int[] values = new int[N];
            for (int i = 0; i < N; i++) {
                weights[i] = random.nextInt(W) + 1;
                values[i] = random.nextInt(C) + 1;
            }

            int res1, res2;
            if ((res1 = maxValue1(weights, values, V)) != (res2 = maxValue2(weights, values, V))) {
                System.err.println(time + ": error { res1: " + res1 + ", res2: " + res2);
            }
        }

    }

    private static int maxValue1(int[] weights, int[] values, int capacity) {
        int[][] dp = new int[weights.length + 1][capacity + 1];
        for (int i = 1; i <= weights.length; i++) {
            for (int v = 1; v <= capacity; v++) {
                if (v < weights[i - 1]) {
                    dp[i][v] = dp[i - 1][v];
                } else {
                    dp[i][v] = Math.max(dp[i - 1][v], dp[i - 1][v - weights[i - 1]] + values[i - 1]);
                }
            }
        }

        return dp[weights.length][capacity];
    }

    private static int maxValue2(int[] weights, int[] values, int capacity) {
        int[] dp = new int[capacity + 1];

        for (int i = 1; i <= weights.length; i++) {
            //这里必须降序遍历，否则将得到错误结果
            for (int v = capacity; v >= 1; v--) {
                if (v < weights[i - 1]) break;
                dp[v] = Math.max(dp[v], dp[v - weights[i - 1]] + values[i - 1]);
            }
        }
        return dp[capacity];
    }
}

2.2 Java源码

对应HihoCode第1081题。可自行验证正确性

package org.liuyehcf.graph;

import java.util.Arrays;
import java.util.Scanner;

/**
 * Created by t-chehe on 8/5/2017.
 */
public class FloydWarshall {
    private static final int CANNOT_REACH = Integer.MAX_VALUE >> 2;

    public static void main(String[] args) {
        //edgeNum并不代表真正有效边的数量，因为相同的源节点和目的节点之间可能有多条道路，我们只需要保留最小的即可
        int vertexNum, edgeNum, source, dest;

        Scanner scanner = new Scanner(System.in);

        vertexNum = scanner.nextInt();
        edgeNum = scanner.nextInt();
        source = scanner.nextInt();
        dest = scanner.nextInt();

        int[][] graph = new int[vertexNum + 1][vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            Arrays.fill(graph[i], CANNOT_REACH);
            graph[i][i] = 0;
        }

        while (--edgeNum >= 0) {
            int s = scanner.nextInt();
            int d = scanner.nextInt();
            int l = scanner.nextInt();

            //题意中的道路是双向都可通的，因此对于有向图来说两个方向都需要存
            if (l < graph[s][d]) {
                graph[s][d] = l;
                graph[d][s] = l;
            }
        }

        System.out.println(minPath2(graph, vertexNum, source, dest));
    }

    public static int minPath1(int[][] graph, int vertexNum, int source, int dest) {
        int dp[][][] = new int[vertexNum + 1][vertexNum + 1][vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            dp[0][i] = graph[i].clone();
        }

        for (int k = 1; k <= vertexNum; k++) {
            for (int i = 1; i <= vertexNum; i++) {
                for (int j = 1; j <= vertexNum; j++) {

                    dp[k][i][j] = Math.min(dp[k - 1][i][j], dp[k - 1][i][k] + dp[k - 1][k][j]);
                }
            }
        }

        return dp[vertexNum][source][dest];
    }

    public static int minPath2(int[][] graph, int vertexNum, int source, int dest) {
        int dp[][] = new int[vertexNum + 1][vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            dp[i] = graph[i].clone();
        }

        //表示DP过程的迭代k必须置于最外层
        for (int k = 1; k <= vertexNum; k++) {
            //必须逆序
            for (int i = vertexNum; i >= 1; i--) {
                for (int j = vertexNum; j >= 1; j--) {

                    dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);

                }
            }
        }

        return dp[source][dest];
    }
}

3 Bellman-Ford

Dijkstra算法是处理单源最短路径的有效算法，但它对存在负权回路的图就会失效。这时候，就需要使用其他的算法来应对这个问题，Bellman-Ford（中文名：贝尔曼-福特）算法就是其中一个

Bellman-Ford算法不仅可以求出最短路径，也可以检测负权回路的问题。该算法由美国数学家理查德-贝尔曼（Richard Bellman，动态规划的提出者）和小莱斯特-福特（Lester Ford）发明

3.1 算法描述

对于一个不存在负权回路的图，Bellman-Ford算法求解最短路径的方法如下：

设其顶点数为n，边数为m。设其源点为source，数组dist[i]记录从源节点source到顶点i的最短路径，除了dist[source]初始化为0外，其它dist[]皆初始化为MAX。以下操作循环执行n-1次：

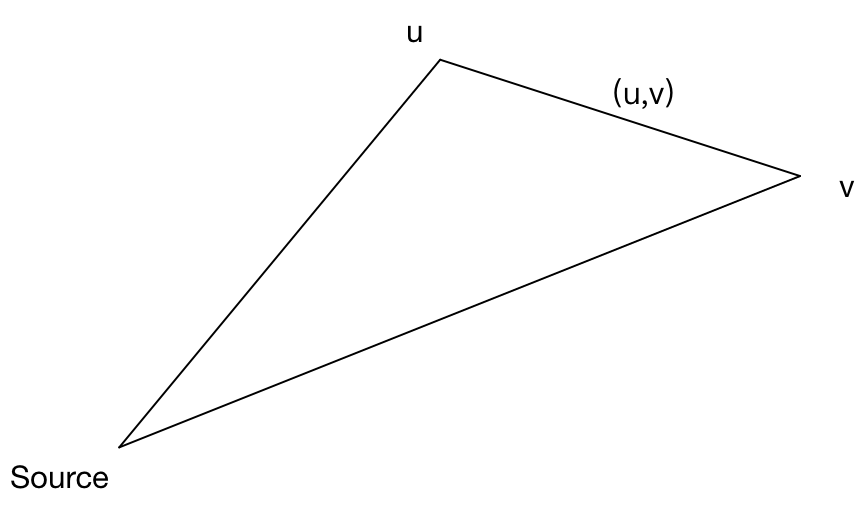
• 对于每条有向边(u,v)，执行dist[v] = min(dist[v], dist[u] + w(u,v))。其含义就是对于某条有向边(u,v)，从源节点source到节点v的最短距离只有两种可能：一种是不经过有向边(u,v)；另一种是经过有向边(u,v)。如下图所示

n-1次循环，Bellman-Ford算法就是利用已经找到的最短路径去更新其它点的dist[]。每次循环能确定一个顶点的最短路径，因此n-1此循环后，dist[]保存的就是源节点到所有顶点的最短路径

此外，Bellman-Ford算法还可以检测是否存在负权边，只要再进行一次循环，如果发现dist[v] > dist[u] + w(u,v)，那么说明存在负权边。因为对于一个不存在负权边的有向图来说，执行n-1次循环与执行m次(m >= n-1)循环得到的dist是相同的

3.2 Java源码

对应HihoCode第1081题。可自行验证正确性

package org.liuyehcf.graph;

import java.util.Arrays;
import java.util.LinkedList;
import java.util.List;
import java.util.Scanner;

/**
 * Created by HCF on 2017/8/6.
 */
public class BellmanFord {
    private static final int CANNOT_REACH = Integer.MAX_VALUE >> 2;

    private static class Edge {
        final int source;

        final int dest;

        int length;

        public Edge(int source, int dest, int length) {
            this.source = source;
            this.dest = dest;
            this.length = length;
        }
    }

    public static void main(String[] args) {
        //edgeNum并不代表真正有效边的数量，因为相同的源节点和目的节点之间可能有多条道路，我们只需要保留最小的即可
        int vertexNum, edgeNum, source, dest;

        Scanner scanner = new Scanner(System.in);

        vertexNum = scanner.nextInt();
        edgeNum = scanner.nextInt();
        source = scanner.nextInt();
        dest = scanner.nextInt();

        int[][] graph = new int[vertexNum + 1][vertexNum + 1];

        for (int i = 1; i <= vertexNum; i++) {
            Arrays.fill(graph[i], CANNOT_REACH);
            graph[i][i] = 0;
        }

        while (--edgeNum >= 0) {
            int s = scanner.nextInt();
            int d = scanner.nextInt();
            int l = scanner.nextInt();

            //题意中的道路是双向都可通的，因此对于有向图来说两个方向都需要存
            if (l < graph[s][d]) {
                graph[s][d] = l;
                graph[d][s] = l;
            }
        }

        List<Edge> edges = new LinkedList<Edge>();

        for (int i = 1; i <= vertexNum; i++) {
            for (int j = 1; j <= vertexNum; j++) {
                if (graph[i][j] < CANNOT_REACH) {
                    edges.add(new Edge(i, j, graph[i][j]));
                }
            }
        }

        System.out.println(minPath(edges, vertexNum, source, dest));
    }

    public static int minPath(List<Edge> edges, int num, int source, int dest) {
        int[] dp = new int[num + 1];

        Arrays.fill(dp, CANNOT_REACH);

        dp[source] = 0;

        for (int k = 1; k < num; k++) {
            for (Edge e : edges) {
                if (e == null) continue;
                dp[e.dest] = Math.min(dp[e.dest], dp[e.source] + e.length);
            }
        }

        return dp[dest];
    }
}

4 参考

• 最短路径—Dijkstra算法和Floyd算法
• 单源最短路径（1）：Dijkstra 算法
• Floyd算法为什么把k放在最外层？
• 百度百科