阅读更多

1 前言

Bloom Filter是由Bloom在1970年提出的一种多哈希函数映射的快速查找算法。通常应用在一些需要快速判断某个元素是否属于集合，但是并不严格要求100%正确的场合

2 问题引入

假设要你写一个网络蜘蛛（web crawler）。由于网络间的链接错综复杂，蜘蛛在网络间爬行很可能会形成环。为了避免形成环，就需要知道蜘蛛已经访问过那些URL。给一个URL，怎样知道蜘蛛是否已经访问过呢？稍微想想，就会有如下几种方案：

将访问过的URL保存到数据库
用HashSet将访问过的URL保存起来。那只需接近O(1)的代价就可以查到一个URL是否被访问过了
URL经过MD5或SHA-1等单向哈希后再保存到HashSet或数据库
Bit-Map方法。建立一个BitSet，将每个URL经过一个哈希函数映射到某一位

方法1~3都是将访问过的URL完整保存，方法4则只标记URL的一个映射位

以上方法在数据量较小的情况下都能完美解决问题，但是当数据量变得非常庞大时问题就来了。

方法1的缺点：数据量变得非常庞大后关系型数据库查询的效率会变得很低。而且每来一个URL就启动一次数据库查询是不是太小题大做了？
方法2的缺点：太消耗内存。随着URL的增多，占用的内存会越来越多。就算只有1亿个URL，每个URL只算50个字符，就需要5GB内存
方法3：由于字符串经过MD5处理后的信息摘要长度只有128Bit，SHA-1处理后也只有160Bit，因此方法3比方法2节省了好几倍的内存
方法4：该方法消耗内存是相对较少的，但缺点是单一哈希函数发生冲突的概率太高。还记得数据结构课上学过的Hash表冲突的各种解决方法么？若要降低冲突发生的概率到1%，就要将BitSet的长度设置为URL个数的100倍

实质上上面的算法都忽略了一个重要的隐含条件：允许小概率的出错，不一定要100%准确！也就是说少量url实际上没有没网络蜘蛛访问，而将它们错判为已访问的代价是很小的——大不了少抓几个网页呗。

其实还有一种方法也可行。我们可以将这海量的URL分成若干份，每份的数量相对较小，单个机器足以处理。那么问题是如何进行分发呢？如果采用随机分发的方式，那么相同的URL可能会被分到不同的机器中，最后整合时还需要在做一次去重操作。另一种方式就是在分发的时候先进行一次聚合操作，所有相同的URL必定被分发到同一个机器上，这样一来，每台机器就可以单独工作，最后进行一次汇总即可。那么如何在分发时进行聚合呢？利用hash函数即可，例如构造一个可以产生m位整数的hash函数，那么m位整数总共有2^m个可能的数值，对每一个URL进行一次hash计算，映射到这其中的一个整数，就分发给对应的机器进行处理

3 Bloom Filter的算法

废话说到这里，下面引入本篇的主角——Bloom Filter。其实上面方法4的思想已经很接近Bloom Filter了。方法四的致命缺点是冲突概率高，为了降低冲突的概念，Bloom Filter使用了多个哈希函数，而不是一个

Bloom Filter算法如下：

创建一个m位BitSet，先将所有位初始化为0，然后选择k个不同的哈希函数。第i个哈希函数对字符串str哈希的结果记为h(i，str)，且h(i，str)的范围是0到m-1

3.1 加入字符串的过程

下面是每个字符串处理的过程，首先是将字符串str记录到BitSet中的过程：

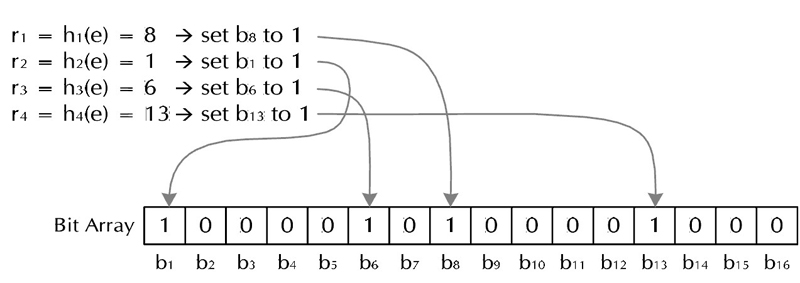
对于字符串str，分别计算h(1, str), h(2, str), ..., h(k, str)。然后将BitSet的第h(1, str), h(2, str), ..., h(k, str)位设为1

3.2 检查字符串是否存在的过程

下面是检查字符串str是否被BitSet记录过的过程：

对于字符串str，分别计算h(1, str), h(2, str), ..., h(k, str)。然后检查BitSet的第h(1, str), h(2, str), ..., h(k, str)位是否为1，若其中任何一位不为1则可以判定str一定没有被记录过。若全部位都是1，则认为字符串str存在

若一个字符串对应的Bit不全为1，则可以肯定该字符串一定没有被Bloom Filter记录过。（这是显然的，因为字符串被记录过，其对应的二进制位肯定全部被设为1了）

但是若一个字符串对应的Bit全为1，实际上是不能100%的肯定该字符串被Bloom Filter记录过的。（因为有可能该字符串的所有位都刚好是被其他字符串所对应）这种将该字符串划分错的情况，称为false positive

3.3 删除字符串过程

字符串加入了就被不能删除了，因为删除会影响到其他字符串。实在需要删除字符串的可以使用Counting bloomfilter(CBF)，这是一种基本Bloom Filter的变体，CBF将基本Bloom Filter每一个Bit改为一个计数器，这样就可以实现删除字符串的功能了

Bloom Filter跟单哈希函数Bit-Map不同之处在于：Bloom Filter使用了k个哈希函数，每个字符串跟k个bit对应。从而降低了冲突的概率

4 Bloom Filter参数选择

哈希函数选择：哈希函数的选择对性能的影响应该是很大的，一个好的哈希函数要能近似等概率的将字符串映射到各个Bit。选择k个不同的哈希函数比较麻烦，一种简单的方法是选择一个哈希函数，然后送入k个不同的参数

Bit数组大小选择：哈希函数个数k、位数组大小m、加入的字符串数量n的关系可以参考Bloom Filters - the math。该文献证明了对于给定的m、n，当k = ln(2)* m/n时出错的概率是最小的

同时该文献还给出特定的k，m，n的出错概率。例如：根据参考文献1，哈希函数个数k取10，位数组大小m设为字符串个数n的20倍时，false positive发生的概率是0.0000889，这个概率基本能满足网络爬虫的需求了

5 Bloom Filter的优化

上面提到的Bloom Filter中的k个hash函数共享同一个BitSet，且他们之间并没有先后次序的关系hash(1, str) = 1, hash(2, str) = 2与hash(1, str) = 2,hash(2, str) = 1的结果是相同的)，这样做实际上会增加重复的概率，因为不同的hash函数可能会让同一个bit置位。因此我们以牺牲空间复杂度为代价，将一个BitSet扩充为k个BitSet，每一个hash独占一个BitSet，这样可以大大降低误判的概率

举个简单的例子，假设BitSet共有4位，有2个hash函数

我们以两个URL进行分析：对于URL1，hash1(URL1) = 1，hash2(URL1) = 2；对于URL2，hash1(URL2) = 2，hash2(URL2) = 1

若2个hash共享同一个BitSet，初始化的时候BitSet = 0000，存入URL1后，BitSet = 0110。此时对于URL2而言，经过两个hash函数映射到第2位和第1位，发现此时BitSet中这两位全是1，因此判定为重复。究其原因，就是因为URL1在存入bit位的时候丢失了部分信息(该位是由哪个hash函数产生的)

若2个hash分别独占一个BitSet，初始化的时候BitSet1 = 0000, BitSet2 = 0000，存入URL1后，BitSet1 = 0100, BitSet2 = 0010。此时对于URL2而言，发现BitSet1的第2位与BitSet2的第1位是0，因此判定没有重复

6 示例代码

#include <bitset>
#include <iostream>

class BloomFilter {
private:
    std::bitset<100> bitArray;
    std::hash<std::string> hashFunc;

public:
    void add(const std::string& item) {
        size_t hash = hashFunc(item);
        size_t index = hash % bitArray.size();
        bitArray[index] = true;
    }

    bool contains(const std::string& item) {
        size_t hash = hashFunc(item);
        size_t index = hash % bitArray.size();
        return bitArray[index];
    }
};

int main() {
    BloomFilter bf;
    bf.add("apple");
    bf.add("banana");

    std::cout << bf.contains("apple") << std::endl;  // Output: 1 (true)
    std::cout << bf.contains("banana") << std::endl; // Output: 1 (true)
    std::cout << bf.contains("orange") << std::endl; // Output: 0 (false)

    return 0;
}

7 参考

BloomFilter——大规模数据处理利器

Liuye Notebook

DataStructure-Bloom-Filter